Published online by Cambridge University Press: 20 November 2018
Let  $K$ be a number field, and let
$K$ be a number field, and let 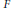 $F$ be a symmetric bilinear form in
$F$ be a symmetric bilinear form in 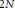 $2N$ variables over
$2N$ variables over  $K$. Let
$K$. Let 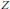 $Z$ be a subspace of
$Z$ be a subspace of 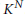 ${{K}^{N}}$. A classical theorem of Witt states that the bilinear space
${{K}^{N}}$. A classical theorem of Witt states that the bilinear space 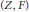 $\left( Z,\,F \right)$ can be decomposed into an orthogonal sum of hyperbolic planes and singular and anisotropic components. We prove the existence of such a decomposition of small height, where all bounds on height are explicit in terms of heights of
$\left( Z,\,F \right)$ can be decomposed into an orthogonal sum of hyperbolic planes and singular and anisotropic components. We prove the existence of such a decomposition of small height, where all bounds on height are explicit in terms of heights of 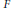 $F$ and
$F$ and 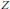 $Z$. We also prove a special version of Siegel's lemma for a bilinear space, which provides a small-height orthogonal decomposition into one-dimensional subspaces. Finally, we prove an effective version of the Cartan-Dieudonné theorem. Namely, we show that every isometry
$Z$. We also prove a special version of Siegel's lemma for a bilinear space, which provides a small-height orthogonal decomposition into one-dimensional subspaces. Finally, we prove an effective version of the Cartan-Dieudonné theorem. Namely, we show that every isometry  $~\sigma$ of a regular bilinear space
$~\sigma$ of a regular bilinear space 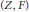 $\left( Z,\,F \right)$ can be represented as a product of reflections of bounded heights with an explicit bound on heights in terms of heights of
$\left( Z,\,F \right)$ can be represented as a product of reflections of bounded heights with an explicit bound on heights in terms of heights of 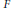 $F$,
$F$, 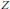 $Z$, and
$Z$, and  $~\sigma$.
$~\sigma$.