No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
The Lp-norm convergence of weighted averages μnf is ergodic theory is equivalent to the pointwise convergence of the Fourier transforms 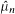 . If h(γ) =
. If h(γ) = 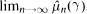 , then the behavior of h determines when the Lp-norm limit of μnf is ∫f dm. The nature of such limit functions h is the focus of this article.
, then the behavior of h determines when the Lp-norm limit of μnf is ∫f dm. The nature of such limit functions h is the focus of this article.