Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schäfer-Nameki, Sakura
Yamazaki, Masahito
and
Yoshida, Kentaroh
2009.
Coset construction for duals of non-relativistic CFTs.
Journal of High Energy Physics,
Vol. 2009,
Issue. 05,
p.
038.
MILSON, R.
and
PELAVAS, N.
2009.
THE CURVATURE HOMOGENEITY BOUND FOR LORENTZIAN FOUR-MANIFOLDS.
International Journal of Geometric Methods in Modern Physics,
Vol. 06,
Issue. 01,
p.
99.
Batat, Wafaa
Calvaruso, Giovanni
and
De Leo, Barbara
2009.
Curvature Properties of Lorentzian Manifolds with Large Isometry Groups.
Mathematical Physics, Analysis and Geometry,
Vol. 12,
Issue. 3,
p.
201.
Dušek, Zdeněk
2010.
The existence of homogeneous geodesics in homogeneous pseudo-Riemannian and affine manifolds.
Journal of Geometry and Physics,
Vol. 60,
Issue. 5,
p.
687.
Batat, Wafaa
Gadea, Pedro M.
and
Oubiña, José A.
2011.
Homogeneous pseudo-Riemannian structures of linear type.
Journal of Geometry and Physics,
Vol. 61,
Issue. 3,
p.
745.
CALVARUSO, GIOVANNI
and
FINO, ANNA
2013.
COMPLEX AND PARACOMPLEX STRUCTURES ON HOMOGENEOUS PSEUDO-RIEMANNIAN FOUR-MANIFOLDS.
International Journal of Mathematics,
Vol. 24,
Issue. 01,
p.
1250130.
Batat, W.
and
Onda, K.
2013.
Four-Dimensional Pseudo-Riemannian Generalized Symmetric Spaces Which are Algebraic Ricci Solitons.
Results in Mathematics,
Vol. 64,
Issue. 3-4,
p.
253.
Calvaruso, Giovanni
and
Zaeim, Amirhesam
2014.
A complete classification of Ricci and Yamabe solitons of non-reductive homogeneous 4-spaces.
Journal of Geometry and Physics,
Vol. 80,
Issue. ,
p.
15.
Calvaruso, Giovanni
and
Zaeim, Amirhesam
2014.
Four-dimensional homogeneous Lorentzian manifolds.
Monatshefte für Mathematik,
Vol. 174,
Issue. 3,
p.
377.
Calvaruso, Giovanni
and
Zaeim, Amirhesam
2015.
Invariant symmetries on non-reductive homogeneous pseudo-Riemannian four-manifolds.
Revista Matemática Complutense,
Vol. 28,
Issue. 3,
p.
599.
Calvaruso, Giovanni
Fino, Anna
and
Zaeim, Amirhesam
2015.
Homogeneous geodesics of non-reductive homogeneous pseudo-Riemannian 4-manifolds.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 46,
Issue. 1,
p.
23.
Luján, Ignacio
2015.
Reductive locally homogeneous pseudo-Riemannian manifolds and Ambrose–Singer connections.
Differential Geometry and its Applications,
Vol. 41,
Issue. ,
p.
65.
Dušek, Zdeněk
2015.
The existence of light‐like homogeneous geodesics in homogeneous Lorentzian manifolds.
Mathematische Nachrichten,
Vol. 288,
Issue. 8-9,
p.
872.
Calvaruso, Giovanni
and
Fino, Anna
2015.
Four-dimensional pseudo-Riemannian homogeneous Ricci solitons.
International Journal of Geometric Methods in Modern Physics,
Vol. 12,
Issue. 05,
p.
1550056.
Calviño‐Louzao, Esteban
García‐Río, Eduardo
Gutiérrez‐Rodríguez, Ixchel
and
Vázquez‐Lorenzo, Ramón
2017.
Conformal geometry of non‐reductive four‐dimensional homogeneous spaces.
Mathematische Nachrichten,
Vol. 290,
Issue. 10,
p.
1470.
Calvaruso, Giovanni
and
Zaeim, Amirhesam
2018.
Four-dimensional pseudo-Riemannian g.o. spaces and manifolds.
Journal of Geometry and Physics,
Vol. 130,
Issue. ,
p.
63.
Alekseevsky, Dmitri
Chrysikos, Ioannis
and
Taghavi-Chabert, Arman
2019.
Decomposable (4, 7) solutions in eleven-dimensional supergravity.
Classical and Quantum Gravity,
Vol. 36,
Issue. 7,
p.
075002.
Zaeim, Amirhesam
Jafari, Mehdi
and
Yaghoubi, Maryam
2020.
Harmonic metrics on Gödel-type spacetimes.
International Journal of Geometric Methods in Modern Physics,
Vol. 17,
Issue. 06,
p.
2050092.
Calvaruso, Giovanni
Storm, Reinier
and
Van der Veken, Joeri
2020.
Parallel and totally geodesic hypersurfaces of non‐reductive homogeneous four‐manifolds.
Mathematische Nachrichten,
Vol. 293,
Issue. 9,
p.
1707.
Chen, Bang-Yen
2020.
Differential Geometry of Identity Maps: A Survey.
Mathematics,
Vol. 8,
Issue. 8,
p.
1264.
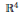 ${{\mathbb{R}}^{4}}$ . All metrics for the simply connected non-reductive Einstein spaces are given explicitly. There are no non-reductive pseudo-Riemannian homogeneous spaces of dimension two and none of dimension three with connected isotropy subgroup.
${{\mathbb{R}}^{4}}$ . All metrics for the simply connected non-reductive Einstein spaces are given explicitly. There are no non-reductive pseudo-Riemannian homogeneous spaces of dimension two and none of dimension three with connected isotropy subgroup.
