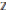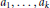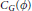Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shalev, Aner
2000.
New Horizons in pro-p Groups.
p.
1.
Shumyatsky, Pavel
2011.
On the exponent of a finite group with an automorphism group of order twelve.
Journal of Algebra,
Vol. 331,
Issue. 1,
p.
482.
Shumyatsky, Pavel
2012.
Exponent of a finite group with a four-group of automorphisms.
Monatshefte für Mathematik,
Vol. 168,
Issue. 1,
p.
113.
Shumyatsky, Pavel
2013.
Exponent of a finite group with a fixed-point-free four-group of automorphisms.
Israel Journal of Mathematics,
Vol. 194,
Issue. 2,
p.
895.