No CrossRef data available.
Article contents
Necessary and Sufficient Conditions for Hypoellipticity for a Class of Convolution Operators
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper the Corwin's conjecture is proved, which says that if d is a function analytic near ∞, then the hypoellipticity of the convolution operator Ad , defined by 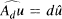 for every u ∊ S'(ℝn ), implies that P(x)/ logx → ∞ as x → ∞, where P(x) is the distance from x ∊ ℝn to the set of complex zeros of d.
for every u ∊ S'(ℝn ), implies that P(x)/ logx → ∞ as x → ∞, where P(x) is the distance from x ∊ ℝn to the set of complex zeros of d.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1994
Footnotes
Supported by NNFC and Special Fund for Doctoral Program in University.
References
1.
Corwin, L., Necessary and Sufficient Conditions for Hypoellipticity for Certain Left Invariant Operators on Nilpotent Groups, Comm. PDE (9)
1(1984), 1–32.Google Scholar
2.
Hormander, L., The Analysis of Linear Partial Differential Operators, If
Springer-Verlag, Berlin, 1983.Google Scholar
3.
Narasimhan, R., Several Complex Variables, The University of Chicago Press, Chicago and London, 1971.Google Scholar
4.
Porter, M. H. and Weinberger, H. F., Maximum Principles in Differential Equations, Prentice-Hall, Englewood Cliffs, New Jersey, 1967.Google Scholar
5.
Barros-Neto, J., An Introduction to the Theory of Distributions, Marcel Dekker, New York, 1973.Google Scholar

