Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hu, Jun
and
Wang, Jianpan
2001.
On simple modules of Hecke algebras of type Dn.
Science in China Series A: Mathematics,
Vol. 44,
Issue. 8,
p.
953.
Cantrell, Andy
Halverson, Tom
and
Miller, Brian
2002.
Robinson–Schensted–Knuth insertion and characters of cyclotomic Hecke algebras.
Journal of Combinatorial Theory, Series A,
Vol. 99,
Issue. 1,
p.
17.
Ram, Arun
and
Ramagge, Jacqui
2003.
A Tribute to C. S. Seshadri.
p.
428.
Hu, Jun
2004.
Modular representations of Hecke algebras of type G(p,p,n).
Journal of Algebra,
Vol. 274,
Issue. 2,
p.
446.
Ding, Jun
and
Hu, Jun
2006.
Lusztig's isomorphism theorem for cellular algebras.
Journal of Pure and Applied Algebra,
Vol. 205,
Issue. 2,
p.
296.
Mak, Chi Kin
2008.
A Reducibility Theorem ofG(m, 1,r) and Its Application to Trace Functions on Ariki–Koike Algebras.
Communications in Algebra,
Vol. 36,
Issue. 3,
p.
973.
Marin, Ivan
2010.
Branching properties for the groups G(de,e,r).
Journal of Algebra,
Vol. 323,
Issue. 4,
p.
966.
Wang, Li
2012.
Erdős-Ko-Rado theorem for irreducible imprimitive reflection groups.
Frontiers of Mathematics in China,
Vol. 7,
Issue. 1,
p.
125.
Ariki, Susumu
Jacon, Nicolas
and
Lecouvey, Cédric
2012.
Factorization of the canonical bases for higher-level Fock spaces.
Proceedings of the Edinburgh Mathematical Society,
Vol. 55,
Issue. 1,
p.
23.
Tewari, Vasu
2016.
A Murnaghan–Nakayama rule for noncommutative Schur functions.
European Journal of Combinatorics,
Vol. 58,
Issue. ,
p.
118.
Giannelli, Eugenio
and
Miller, Alexander R.
2019.
Character restrictions and reflection groups.
Journal of Algebra,
Vol. 531,
Issue. ,
p.
336.
Mishra, Ashish
and
Srivastava, Shraddha
2020.
On representation theory of partition algebras for complex reflection groups.
Algebraic Combinatorics,
Vol. 3,
Issue. 2,
p.
389.
Mishra, Ashish
Paul, Digjoy
and
Singla, Pooja
2023.
On Quasi Steinberg Characters of Complex Reflection Groups.
Algebras and Representation Theory,
Vol. 26,
Issue. 6,
p.
3101.
Jing, Naihuan
and
Liu, Ning
2023.
Murnaghan–Nakayama Rule and Spin Bitrace for the Hecke–Clifford Algebra.
International Mathematics Research Notices,
Vol. 2023,
Issue. 19,
p.
17060.
Mazorchuk, Volodymyr
and
Srivastava, Shraddha
2024.
Multiparameter colored partition category and the product of the reduced Kronecker coefficients.
Journal of Pure and Applied Algebra,
Vol. 228,
Issue. 3,
p.
107524.
Nguyen, Duc-Khanh
2024.
A Generalization of the Murnaghan–Nakayama Rule for K-k-Schur and k-Schur Functions.
International Mathematics Research Notices,
Vol. 2024,
Issue. 6,
p.
4738.
Zhao, Deke
2025.
Characters of Ariki–Koike algebras.
Journal of Algebra,
Vol. 684,
Issue. ,
p.
773.
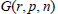 $G(r,\,p,\,n)$ were constructed recently in the work of Ariki and Koike [AK], Broué and Malle [BM], and Ariki [Ari]. In this paper we give Murnaghan-Nakayama type formulas for computing the irreducible characters of these algebras. Our method is a generalization of that in our earlier paper [HR] in which we derived Murnaghan-Nakayama rules for the characters of the Iwahori-Hecke algebras of the classical Weyl groups. In both papers we have been motivated by C. Greene [Gre], who gave a new derivation of the Murnaghan-Nakayama formula for irreducible symmetric group characters by summing diagonal matrix entries in Young's seminormal representations. We use the analogous representations of the Iwahori-Hecke algebra of
$G(r,\,p,\,n)$ were constructed recently in the work of Ariki and Koike [AK], Broué and Malle [BM], and Ariki [Ari]. In this paper we give Murnaghan-Nakayama type formulas for computing the irreducible characters of these algebras. Our method is a generalization of that in our earlier paper [HR] in which we derived Murnaghan-Nakayama rules for the characters of the Iwahori-Hecke algebras of the classical Weyl groups. In both papers we have been motivated by C. Greene [Gre], who gave a new derivation of the Murnaghan-Nakayama formula for irreducible symmetric group characters by summing diagonal matrix entries in Young's seminormal representations. We use the analogous representations of the Iwahori-Hecke algebra of 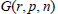 $G(r,\,p,\,n)$ given by Ariki and Koike [AK] and Ariki [Ari].
$G(r,\,p,\,n)$ given by Ariki and Koike [AK] and Ariki [Ari].
