Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Barletta, Giuseppina
and
Papageorgiou, Nikolaos S.
2007.
A multiplicity theorem for the Neumann p-Laplacian with an asymmetric nonsmooth potential.
Journal of Global Optimization,
Vol. 39,
Issue. 3,
p.
365.
Aizicovici, Sergiu
Papageorgiou, Nikolaos S.
and
Staicu, Vasile
2009.
Existence of multiple solutions with precise sign information for superlinear Neumann problems.
Annali di Matematica Pura ed Applicata,
Vol. 188,
Issue. 4,
p.
679.
O’Regan, Donal
and
Papageorgiou, Nikolaos S.
2009.
The existence of two nontrivial solutions via homological local linking for the non-coercive p-Laplacian Neumann problem.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 12,
p.
4386.
Gasiński, Leszek
and
Papageorgiou, Nikolaos S.
2009.
Nontrivial solutions for a class of resonant -Laplacian Neumann problems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 12,
p.
6365.
Iannizzotto, Antonio
and
Papageorgiou, Nikolaos S.
2009.
Existence of three nontrivial solutions for nonlinear Neumann hemivariational inequalities.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 9,
p.
3285.
Papageorgiou, N S
and
Smyrlis, G
2010.
Multiple solutions for nonlinear Neumann problems with thep-Laplacian and a nonsmooth crossing potential.
Nonlinearity,
Vol. 23,
Issue. 3,
p.
529.
Molica Bisci, Giovanni
and
Rădulescu, Vicenţiu D.
2015.
Applications of local linking to nonlocal Neumann problems.
Communications in Contemporary Mathematics,
Vol. 17,
Issue. 01,
p.
1450001.
Colasuonno, Francesca
and
Noris, Benedetta
2017.
A <i>p</i>-Laplacian supercritical Neumann problem.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 6,
p.
3025.
Jiang, Qin
Ma, Sheng
and
Paşca, Daniel
2019.
Existence and Multiplicity of Solutions for p-Laplacian Neumann Problems.
Results in Mathematics,
Vol. 74,
Issue. 1,
Moameni, Abbas
and
Salimi, Leila
2019.
Existence results for a supercritical Neumann problem with a convex–concave non-linearity.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 198,
Issue. 4,
p.
1165.
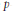 $p$-Laplacian differential operator. We look for situations guaranteeing the existence of multiple solutions. First we study problems which are strongly resonant at infinity at the first (zero) eigenvalue. We prove five multiplicity results, four for problems with nonsmooth potential and one for problems with a
$p$-Laplacian differential operator. We look for situations guaranteeing the existence of multiple solutions. First we study problems which are strongly resonant at infinity at the first (zero) eigenvalue. We prove five multiplicity results, four for problems with nonsmooth potential and one for problems with a 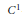 ${{C}^{1}}$-potential. In the last part, for nonsmooth problems in which the potential eventually exhibits a strict super-
${{C}^{1}}$-potential. In the last part, for nonsmooth problems in which the potential eventually exhibits a strict super-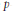 $p$-growth under a symmetry condition, we prove the existence of infinitely many pairs of nontrivial solutions. Our approach is variational based on the critical point theory for nonsmooth functionals. Also we present some results concerning the first two elements of the spectrum of the negative
$p$-growth under a symmetry condition, we prove the existence of infinitely many pairs of nontrivial solutions. Our approach is variational based on the critical point theory for nonsmooth functionals. Also we present some results concerning the first two elements of the spectrum of the negative 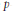 $p$-Laplacian with Neumann boundary condition.
$p$-Laplacian with Neumann boundary condition.