No CrossRef data available.
Article contents
Monotonically Controlled Mappings
Published online by Cambridge University Press: 20 November 2018
Abstract
We study classes of mappings between finite and infinite dimensional Banach spaces that are monotone and mappings which are differences of monotone mappings ( 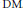 $\text{DM}$ ). We prove a Radó–Reichelderfer estimate for monotone mappings in finite dimensional spaces that remains valid for
$\text{DM}$ ). We prove a Radó–Reichelderfer estimate for monotone mappings in finite dimensional spaces that remains valid for 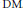 $\text{DM}$ mappings. This provides an alternative proof of the Fréchet differentiability a.e. of
$\text{DM}$ mappings. This provides an alternative proof of the Fréchet differentiability a.e. of 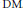 $\text{DM}$ mappings. We establish a Morrey-type estimate for the distributional derivative of monotone mappings. We prove that a locally
$\text{DM}$ mappings. We establish a Morrey-type estimate for the distributional derivative of monotone mappings. We prove that a locally 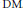 $\text{DM}$ mapping between finite dimensional spaces is also globally
$\text{DM}$ mapping between finite dimensional spaces is also globally 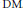 $\text{DM}$ . We introduce and study a new class of the so-called
$\text{DM}$ . We introduce and study a new class of the so-called 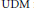 $\text{UDM}$ mappings between Banach spaces, which generalizes the concept of curves of finite variation.
$\text{UDM}$ mappings between Banach spaces, which generalizes the concept of curves of finite variation.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012

