No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In a 2012 paper, the second author showed that a tunnel of a tunnel number one, fibered link in 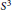 ${{S}^{3}}$ can be isotoped to lie as a properly embedded arc in the fiber surface of the link. In this paper we observe that this is true for fibered links in any 3-manifold, we analyze how the arc behaves under the monodromy action, and we show that the tunnel arc is nearly clean, with the possible exception of twisting around the boundary of the fiber.
${{S}^{3}}$ can be isotoped to lie as a properly embedded arc in the fiber surface of the link. In this paper we observe that this is true for fibered links in any 3-manifold, we analyze how the arc behaves under the monodromy action, and we show that the tunnel arc is nearly clean, with the possible exception of twisting around the boundary of the fiber.