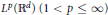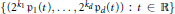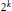Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guo, Shaoming
Hickman, Jonathan
Lie, Victor
and
Roos, Joris
2017.
Maximal operators and Hilbert transforms along variable non‐flat homogeneous curves.
Proceedings of the London Mathematical Society,
Vol. 115,
Issue. 1,
p.
177.
Liu, Naijia
Song, Liang
and
Yu, Haixia
2021.
L bounds of maximal operators along variable planar curves in the Lipschitz regularity.
Journal of Functional Analysis,
Vol. 280,
Issue. 5,
p.
108888.
Yu, Haixia
2022.
Maximal Functions Along Convex Curves with Lacunary Directions.
Taiwanese Journal of Mathematics,
Vol. 26,
Issue. 3,
Oh, Jeongtae
and
Kim, Joonil
2024.
Maximal functions associated to a family of flat curves in lacunary directions.
Mathematische Zeitschrift,
Vol. 306,
Issue. 3,