Article contents
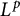 $L^p$-regularity of the Bergman projection on quotient domains
$L^p$-regularity of the Bergman projection on quotient domains
Published online by Cambridge University Press: 08 February 2021
Abstract
We obtain sharp ranges of 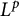 $L^p$-boundedness for domains in a wide class of Reinhardt domains representable as sublevel sets of monomials, by expressing them as quotients of simpler domains. We prove a general transformation law relating
$L^p$-boundedness for domains in a wide class of Reinhardt domains representable as sublevel sets of monomials, by expressing them as quotients of simpler domains. We prove a general transformation law relating 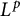 $L^p$-boundedness on a domain and its quotient by a finite group. The range of p for which the Bergman projection is
$L^p$-boundedness on a domain and its quotient by a finite group. The range of p for which the Bergman projection is 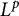 $L^p$-bounded on our class of Reinhardt domains is found to shrink as the complexity of the domain increases .
$L^p$-bounded on our class of Reinhardt domains is found to shrink as the complexity of the domain increases .
MSC classification
Primary:
32A36: Bergman spaces
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
Chase Bender was supported by a Student Research and Creative Endeavors grant from Central Michigan University.
Debraj Chakrabarti was partially supported by National Science Foundation grant DMS-1600371.
References
Axler, S.,
Bergman spaces and their operators
. In: Surveys of some recent results in operator theory, Vol. I, Pitman Res. Notes Math. Ser., 171, Longman Sci. Tech., Harlow, 1988, pp. 1–50.Google Scholar
Barrett, D. and Şahutoğlu, S.,
Irregularity of the Bergman projection on worm domains in
 ${\mathbb{C}}^n$
. Michigan Math. J. 61(2012), no. 1, 187–198.CrossRefGoogle Scholar
${\mathbb{C}}^n$
. Michigan Math. J. 61(2012), no. 1, 187–198.CrossRefGoogle Scholar
Barrett, D. E.,
Irregularity of the Bergman projection on a smooth bounded domain in C2
. Ann. Math. (2) 119(1984), no. 2, 431–436.CrossRefGoogle Scholar
Behnke, H.,
Zur Theorie der Singularitäten der Funktionen mehrerer komplexen Veränderlichen
. Math. Ann. 108(1933), no. 1, 91–104.CrossRefGoogle Scholar
Bell, S. and Catlin, D.,
Boundary regularity of proper holomorphic mappings
. Duke Math. J. 49(1982), no. 2, 385–396.CrossRefGoogle Scholar
Bell, S. R.,
Proper holomorphic mappings and the Bergman projection
. Duke Math. J. 48(1981), no. 1, 167–175.CrossRefGoogle Scholar
Bell, S. R.,
The Bergman kernel function and proper holomorphic mappings
. Trans. Amer. Math. Soc. 270(1982), no. 2, 685–691.Google Scholar
Catlin, D.,
Boundary behavior of holomorphic functions on pseudoconvex domains
. J. Differential Geom. 15(1980/1981), no. 4, 605–625.CrossRefGoogle Scholar
Chakrabarti, D.,
On an observation of Sibony
. Proc. Amer. Math. Soc. 147(2019), no. 8, 3451–3454.CrossRefGoogle Scholar
Chakrabarti, D., Edholm, L. D., and McNeal, J. D.,
Duality and approximation of Bergman spaces
. Adv. Math. 341(2019), 616–656.CrossRefGoogle Scholar
Chakrabarti, D., Konkel, A., Mainkar, M., and Miller, E.,
Bergman kernels of elementary Reinhardt domains
. Pacific J. Math. 306(2020), no. 1, 67–93.CrossRefGoogle Scholar
Chakrabarti, D. and Zeytuncu, Y. E.,
Lp mapping properties of the Bergman projection on the Hartogs triangle
. Proc. Amer. Math. Soc. 144(2016), no. 4, 1643–1653.CrossRefGoogle Scholar
Chen, L.,
The
 ${L}^p$
boundedness of the Bergman projection for a class of bounded Hartogs domains
. J. Math. Anal. Appl. 448(2017), no. 1, 598–610.CrossRefGoogle Scholar
${L}^p$
boundedness of the Bergman projection for a class of bounded Hartogs domains
. J. Math. Anal. Appl. 448(2017), no. 1, 598–610.CrossRefGoogle Scholar
Chen, L., Jin, M., and Yuan, Y., Bergman projection on the symmetrized bidisk. Preprint, 2020. arXiv:2004.02785.Google Scholar
Chen, L., Krantz, S. G., and Yuan, Y.,
Lp regularity of the Bergman projection on domains covered by the polydisc
. J. Funct. Anal. 279(2020), no. 2, 108522.CrossRefGoogle Scholar
Collatz, L., Functional analysis and numerical mathematics. Academic Press, New York, London, 1966. Translated from the German by Hansjörg Oser.Google Scholar
Diederich, K. and Fornaess, J. E.,
Boundary regularity of proper holomorphic mappings
. Invent. Math. 67(1982), no. 3, 363–384.CrossRefGoogle Scholar
Dummit, D. S. and Foote, R. M., Abstract algebra. 3rd ed., John Wiley & Sons, Inc., Hoboken, NJ, 2004.Google Scholar
Duren, P. and Schuster, A.,
Bergman spaces
. Mathematical Surveys and Monographs, 100, American Mathematical Society, Providence, RI, 2004.CrossRefGoogle Scholar
Edholm, L. D.,
Bergman theory of certain generalized Hartogs triangles
.
Pacific J. Math.
284(2016), no. 2, 327–342.CrossRefGoogle Scholar
Edholm, L. D. and McNeal, J. D.,
The Bergman projection on fat Hartogs triangles:
 ${L}^p$
boundedness
.
Proc. Amer. Math. Soc.
144(2016), no. 5, 2185–2196.CrossRefGoogle Scholar
${L}^p$
boundedness
.
Proc. Amer. Math. Soc.
144(2016), no. 5, 2185–2196.CrossRefGoogle Scholar
Edholm, L. D. and McNeal, J. D.,
Bergman subspaces and subkernels: degenerate
 ${L}^p$
mapping and zeroes
.
J. Geom. Anal.
27(2017), no. 4, 2658–2683.CrossRefGoogle Scholar
${L}^p$
mapping and zeroes
.
J. Geom. Anal.
27(2017), no. 4, 2658–2683.CrossRefGoogle Scholar
Edholm, L. D. and McNeal, J. D.,
Sobolev mapping of some holomorphic projections
.
J. Geom. Anal.
30(2020), no. 2, 1293–1311.CrossRefGoogle Scholar
Forelli, F. and Rudin, W.,
Projections on spaces of holomorphic functions in balls
.
Indiana Univ. Math. J.
, 24(1974/1975), 593–602.CrossRefGoogle Scholar
Grünbaum, B.,
Convex polytopes.
2nd ed., Graduate Texts in Mathematics, 221, Springer-Verlag, New York, 2003. Prepared and with a preface by Volker Kaibel, Victor Klee and Günter M. Ziegler.CrossRefGoogle Scholar
Hakim, M. and Sibony, N.,
Spectre de
 $A\left(\bar{\varOmega}\right)$
pour des domaines bornés faiblement pseudoconvexes réguliers
.
J. Funct. Anal.
37(1980), no. 2, 127–135.CrossRefGoogle Scholar
$A\left(\bar{\varOmega}\right)$
pour des domaines bornés faiblement pseudoconvexes réguliers
.
J. Funct. Anal.
37(1980), no. 2, 127–135.CrossRefGoogle Scholar
Hedenmalm, H.,
The dual of a Bergman space on simply connected domains
.
J. Anal. Math.
88(2002), 311–335.CrossRefGoogle Scholar
Hedenmalm, H., Korenblum, B., and Zhu, K.,
Theory of Bergman spaces
. Graduate Texts in Mathematics, 199, Springer-Verlag, New York, 2000.CrossRefGoogle Scholar
Hindry, M. and Silverman, J. H.,
Diophantine geometry
. Graduate Texts in Mathematics, 201, Springer-Verlag, New York, 2000. An introduction.CrossRefGoogle Scholar
Huo, Z.,
Lp estimates for the Bergman projection on some Reinhardt domains
.
Proc. Amer. Math. Soc.
146(2018), no. 6, 2541–2553.CrossRefGoogle Scholar
Huo, Z. and Wick, B. D., Weak-type estimates for the Bergman projection on the polydisc and the Hartogs triangle. Preprint, 2019. arXiv:1909.05902.CrossRefGoogle Scholar
Jarnicki, M. and Pflug, P.,
First steps in several complex variables: Reinhardt domains
. EMS Textbooks in Mathematics, European Mathematical Society (EMS), Zürich, 2008.CrossRefGoogle Scholar
Kobayashi, S.,
Geometry of bounded domains
.
Trans. Amer. Math. Soc.
92(1959), 267–290.CrossRefGoogle Scholar
Krantz, S. G.,
Geometric analysis of the Bergman kernel and metric
. Graduate Texts in Mathematics, 268, Springer, New York, 2013.CrossRefGoogle Scholar
Krantz, S. G. and Peloso, M. M.,
Analysis and geometry on worm domains
.
J. Geom. Anal.
18(2008), no. 2, 478–510.CrossRefGoogle Scholar
Massey, W. S.,
A basic course in algebraic topology. Graduate Texts in Mathematics, 127, Springer-Verlag, New York, 1991.CrossRefGoogle Scholar
McNeal, J. D. and Stein, E. M.,
Mapping properties of the Bergman projection on convex domains of finite type
.
Duke Math. J.
73(1994), no. 1, 177–199.CrossRefGoogle Scholar
Misra, G., Roy, S. S., and Zhang, G.,
Reproducing kernel for a class of weighted Bergman spaces on the symmetrized polydisc
.
Proc. Amer. Math. Soc.
141(2013), no. 7, 2361–2370.CrossRefGoogle Scholar
Munkres, J. R.,
Elements of algebraic topology. Addison-Wesley Publishing Company, Menlo Park, CA, 1984.Google Scholar
Nagel, A. and Pramanik, M.,
Maximal averages over linear and monomial polyhedra
.
Duke Math. J.
149(2009), no. 2, 209–277.CrossRefGoogle Scholar
Nagel, A. and Pramanik, M.,
Bergman spaces under maps of monomial type
.
J. Geometr. Anal.
31(2021), no. 5, 4531–4560.CrossRefGoogle Scholar
Park, J.-D.,
The explicit forms and zeros of the Bergman kernel for 3-dimensional Hartogs triangles
.
J. Math. Anal. Appl.
460(2018), no. 2, 954–975.CrossRefGoogle Scholar
Phong, D. H. and Stein, E. M.,
Estimates for the Bergman and Szegö projections on strongly pseudo-convex domains
.
Duke Math. J.
44(1977), no. 3, 695–704.CrossRefGoogle Scholar
Sibony, N.,
Prolongement des fonctions holomorphes bornées et métrique de Carathéodory
.
Invent. Math.
29(1975), no. 3, 205–230.CrossRefGoogle Scholar
Vladimirov, V. S.,
Methods of the theory of functions of many complex variables. The M.I.T. Press, Cambridge, MA, London, 1966. Translated from the Russian by Scripta Technica, Inc. Translation edited by Leon Ehrenpreis.Google Scholar
Zaharjuta, V. P. and Judovic, V. I.,
The general form of a linear functional on
 ${H}_p^{\prime }$
.
Uspekhi Mat. Nauk.
19(1964), no. 2, 139–142.Google Scholar
${H}_p^{\prime }$
.
Uspekhi Mat. Nauk.
19(1964), no. 2, 139–142.Google Scholar
Zhang, S., Mapping properties of the Bergman projections on elementary Reinhardt domains. Submitted, 2019.Google Scholar
Zhang, S.,
Lp boundedness for the Bergman projections over
 $n$
-dimensional generalized Hartogs triangles
.
Complex Var. Elliptic Equ.
(2020). https://doi.org/10.1080/17476933.2020.1769085.Google Scholar
$n$
-dimensional generalized Hartogs triangles
.
Complex Var. Elliptic Equ.
(2020). https://doi.org/10.1080/17476933.2020.1769085.Google Scholar
Ziegler, G. M.,
Lectures on polytopes. Graduate Texts in Mathematics, 152, Springer-Verlag, New York, 1995.CrossRefGoogle Scholar
Zwonek, W.,
On hyperbolicity of pseudoconvex Reinhardt domains
.
Arch. Math. (Basel)
72(1999), no. 4, 304–314.CrossRefGoogle Scholar
Zwonek, W.,
Completeness, Reinhardt domains and the method of complex geodesics in the theory of invariant functions
.
Dissertationes Math. (Rozprawy Mat.)
388(2000), 103.Google Scholar
- 15
- Cited by


