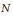Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brauchart, Johann S.
and
Grabner, Peter J.
2015.
Distributing many points on spheres: Minimal energy and designs.
Journal of Complexity,
Vol. 31,
Issue. 3,
p.
293.
Amore, Paolo
and
Jacobo, Martin
2019.
Thomson problem in one dimension: Minimal energy configurations of N charges on a curve.
Physica A: Statistical Mechanics and its Applications,
Vol. 519,
Issue. ,
p.
256.
Hardin, Douglas
Saff, Edward B.
Shu, Ruiwen
and
Tadmor, Eitan
2021.
Dynamics of particles on a curve with pairwise hyper-singular repulsion.
Discrete & Continuous Dynamical Systems,
Vol. 41,
Issue. 12,
p.
5509.
Yao, Zhenwei
2023.
Charged elastic rings: deformation and dynamics.
Journal of Physics: Condensed Matter,
Vol. 35,
Issue. 4,
p.
045101.
Brauchart, J. S.
2024.
Complete Minimal Logarithmic Energy Asymptotics for Points in a Compact Interval: A Consequence of the Discriminant of Jacobi Polynomials.
Constructive Approximation,
Vol. 59,
Issue. 3,
p.
717.