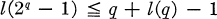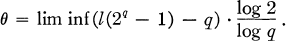Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Thurber, Edward G.
1976.
Addition chains and solutions of l(2n) = l(n) and l(2n − 1) = n + l(n) − 1.
Discrete Mathematics,
Vol. 16,
Issue. 3,
p.
279.
Stolarsky, Kenneth B.
1977.
Power and Exponential Sums of Digital Sums Related to Binomial Coefficient Parity.
SIAM Journal on Applied Mathematics,
Vol. 32,
Issue. 4,
p.
717.
Guy, Richard K.
1981.
Unsolved Problems in Number Theory.
p.
58.
Aiello, Walter
and
Subbarao, M. V.
1993.
A conjecture in addition chains related to Scholz’s conjecture.
Mathematics of Computation,
Vol. 61,
Issue. 203,
p.
17.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
105.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
159.
Clift, Neill Michael
2011.
Calculating optimal addition chains.
Computing,
Vol. 91,
Issue. 3,
p.
265.
Altman, Harry
2018.
Internal structure of addition chains: Well-ordering.
Theoretical Computer Science,
Vol. 721,
Issue. ,
p.
54.