No CrossRef data available.
Article contents
Loops in the fundamental group of 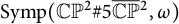 ${\mbox{Symp}} ({\mathbb C}{\mathbb P}^2\# \mbox{5}\overline { \mathbb C\mathbb P}\,\!^2,\omega )$ which are not represented by circle actions
${\mbox{Symp}} ({\mathbb C}{\mathbb P}^2\# \mbox{5}\overline { \mathbb C\mathbb P}\,\!^2,\omega )$ which are not represented by circle actions
Published online by Cambridge University Press: 30 June 2022
Abstract
We study generators of the fundamental group of the group of symplectomorphisms 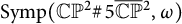 $\operatorname {\mathrm{Symp}} (\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2, \omega )$ for some particular symplectic forms. It was observed by Kȩdra (2009, Archivum Mathematicum 45) that there are many symplectic 4-manifolds
$\operatorname {\mathrm{Symp}} (\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2, \omega )$ for some particular symplectic forms. It was observed by Kȩdra (2009, Archivum Mathematicum 45) that there are many symplectic 4-manifolds 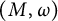 $(M, \omega )$, where M is neither rational nor ruled, that admit no circle action and
$(M, \omega )$, where M is neither rational nor ruled, that admit no circle action and 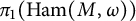 $\pi _1 (\operatorname {\mathrm {Ham}} (M,\omega ))$ is nontrivial. On the other hand, it follows from Abreu and McDuff (2000, Journal of the American Mathematical Society 13, 971–1009), Anjos and Eden (2019, Michigan Mathematical Journal 68, 71–126), Anjos and Pinsonnault (2013, Mathematische Zeitschrift 275, 245–292), and Pinsonnault (2008, Compositio Mathematica 144, 787–810) that the fundamental group of the group
$\pi _1 (\operatorname {\mathrm {Ham}} (M,\omega ))$ is nontrivial. On the other hand, it follows from Abreu and McDuff (2000, Journal of the American Mathematical Society 13, 971–1009), Anjos and Eden (2019, Michigan Mathematical Journal 68, 71–126), Anjos and Pinsonnault (2013, Mathematische Zeitschrift 275, 245–292), and Pinsonnault (2008, Compositio Mathematica 144, 787–810) that the fundamental group of the group  $ \operatorname {\mathrm{Symp}}_h(\mathbb C\mathbb P^2\#\,k\overline { \mathbb C\mathbb P}\,\!^2,\omega )$, of symplectomorphisms that act trivially on homology, with
$ \operatorname {\mathrm{Symp}}_h(\mathbb C\mathbb P^2\#\,k\overline { \mathbb C\mathbb P}\,\!^2,\omega )$, of symplectomorphisms that act trivially on homology, with 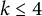 $k \leq 4$, is generated by circle actions on the manifold. We show that, for some particular symplectic forms
$k \leq 4$, is generated by circle actions on the manifold. We show that, for some particular symplectic forms 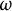 $\omega $, the set of all Hamiltonian circle actions generates a proper subgroup in
$\omega $, the set of all Hamiltonian circle actions generates a proper subgroup in 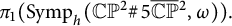 $\pi _1(\operatorname {\mathrm{Symp}}_{h}(\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2,\omega )).$ Our work depends on Delzant classification of toric symplectic manifolds, Karshon’s classification of Hamiltonian
$\pi _1(\operatorname {\mathrm{Symp}}_{h}(\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2,\omega )).$ Our work depends on Delzant classification of toric symplectic manifolds, Karshon’s classification of Hamiltonian 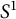 $S^1$-spaces, and the computation of Seidel elements of some circle actions.
$S^1$-spaces, and the computation of Seidel elements of some circle actions.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The first author is partially supported by FCT/Portugal through projects UID/MAT/04459/2019 and PTDC/MAT-PUR/29447/2017. The third author is partially supported by NSERC Discovery Grant RGPIN-2020-06428. All authors except the third are supported by the Calouste Gulbenkian Foundation through the program “New Talents in Mathematics.”


