Article contents
Long Sets of Lengths With Maximal Elasticity
Published online by Cambridge University Press: 20 November 2018
Abstract
We introduce a newinvariant describing the structure of sets of lengths in atomicmonoids and domains. For an atomic monoid  $H$ , let
$H$ , let 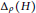 ${{\Delta }_{\rho }}\left( H \right)$ be the set of all positive integers d that occur as differences of arbitrarily long arithmetical progressions contained in sets of lengths havingmaximal elasticity
${{\Delta }_{\rho }}\left( H \right)$ be the set of all positive integers d that occur as differences of arbitrarily long arithmetical progressions contained in sets of lengths havingmaximal elasticity 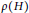 $\rho \left( H \right)$ . We study
$\rho \left( H \right)$ . We study 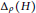 ${{\Delta }_{\rho }}\left( H \right)$ for transfer Krull monoids of finite type (including commutative Krull domains with finite class group) with methods from additive combinatorics, and also for a class of weakly Krull domains (including orders in algebraic number fields) for which we use ideal theoretic methods.
${{\Delta }_{\rho }}\left( H \right)$ for transfer Krull monoids of finite type (including commutative Krull domains with finite class group) with methods from additive combinatorics, and also for a class of weakly Krull domains (including orders in algebraic number fields) for which we use ideal theoretic methods.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2018
References
- 10
- Cited by

