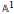Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jardine, J.F.
2000.
Presheaves of symmetric spectra.
Journal of Pure and Applied Algebra,
Vol. 150,
Issue. 2,
p.
137.
Beke, Tibor
2001.
Sheafifiable homotopy model categories, II.
Journal of Pure and Applied Algebra,
Vol. 164,
Issue. 3,
p.
307.
Dwyer, W. G.
2004.
Axiomatic, Enriched and Motivic Homotopy Theory.
p.
3.
Jardine, J. F.
2004.
Axiomatic, Enriched and Motivic Homotopy Theory.
p.
29.
Davis, Daniel G.
2006.
Homotopy fixed points for LK(n)(En∧X) using the continuous action.
Journal of Pure and Applied Algebra,
Vol. 206,
Issue. 3,
p.
322.
Jardine, J. F.
2006.
Intermediate Model Structures for Simplicial Presheaves.
Canadian Mathematical Bulletin,
Vol. 49,
Issue. 3,
p.
407.
Jardine, J. F.
2006.
Diagrams and torsors.
K-Theory,
Vol. 37,
Issue. 3,
p.
291.
Voevodsky, Vladimir
Röndigs, Oliver
and
Østvær, Paul Arne
2007.
Motivic Homotopy Theory.
p.
147.
Neumann, Frank
and
Rodríguez, José L.
2007.
On cellularization for simplicial presheaves and motivic homotopy.
Topology and its Applications,
Vol. 154,
Issue. 7,
p.
1481.
Levine, Marc
2008.
The homotopy coniveau tower.
Journal of Topology,
Vol. 1,
Issue. 1,
p.
217.
Röndigs, Oliver
and
Østvær, Paul Arne
2008.
Rigidity in motivic homotopy theory.
Mathematische Annalen,
Vol. 341,
Issue. 3,
p.
651.
Wendt, Matthias
2013.
Fibre sequences and localization of simplicial sheaves.
Algebraic & Geometric Topology,
Vol. 13,
Issue. 3,
p.
1779.
Dai, Shouxin
and
Levine, Marc
2014.
Connective AlgebraicK-theory.
Journal of K-Theory,
Vol. 13,
Issue. 1,
p.
9.
Guletskiĭ, Vladimir
2016.
$$\mathbb {A}^{1}$$ A 1 -connectivity on Chow monoids versus rational equivalence of algebraic cycles.
European Journal of Mathematics,
Vol. 2,
Issue. 1,
p.
169.
Stelzer, Manfred
2019.
Purity and homotopy theory of coalgebras.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 6,
p.
2455.
Zanchetta, Ferdinando
2021.
Unstable operations on K-theory for singular schemes.
Advances in Mathematics,
Vol. 384,
Issue. ,
p.
107716.