No CrossRef data available.
Article contents
Large values of Dirichlet L-functions at zeros of a class of L-functions
Published online by Cambridge University Press: 01 July 2020
Abstract
In this paper, we are interested in obtaining large values of Dirichlet L-functions evaluated at zeros of a class of L-functions, that is, $$ \begin{align*}\max_{\substack{F(\rho)=0\\ T\leq \Im \rho \leq 2T}}L(\rho,\chi), \end{align*} $$where 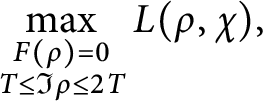
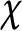 $\chi $ is a primitive Dirichlet character and F belongs to a class of L-functions. The class we consider includes L-functions associated with automorphic representations of
$\chi $ is a primitive Dirichlet character and F belongs to a class of L-functions. The class we consider includes L-functions associated with automorphic representations of 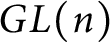 $GL(n)$ over
$GL(n)$ over 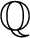 ${\mathbb {Q}}$.
${\mathbb {Q}}$.
Keywords
MSC classification
Primary:
11M06: $zeta (s)$ and $L(s, chi)$
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
Aistleitner, C. and Pańkowski, Ł.,
Large values of
 $L$
-functions from the Selberg class
. J. Math. Anal. Appl. 446(2017), 345–364. https://doi.org/10.1016/j.jmaa.2016.08.044
CrossRefGoogle Scholar
$L$
-functions from the Selberg class
. J. Math. Anal. Appl. 446(2017), 345–364. https://doi.org/10.1016/j.jmaa.2016.08.044
CrossRefGoogle Scholar
Balasubramanian, R. and Ramachandra, K.,
On the frequency of Titchmarsh’s phenomenon for
 $\zeta (s)$
.
III. Proc. Indian Acad. Sci. Sect. A 86(1977), 341–351.CrossRefGoogle Scholar
$\zeta (s)$
.
III. Proc. Indian Acad. Sci. Sect. A 86(1977), 341–351.CrossRefGoogle Scholar
Banks, W.,
Twisted symmetric-square
 $L$
-functions and the nonexistence of Siegel zeros on
$L$
-functions and the nonexistence of Siegel zeros on
 $\mathrm{GL}(3)$
. Duke Math. J. 87(1997), 343–353. https://doi.org/10.1215/S0012-7094-97-08713-5
CrossRefGoogle Scholar
$\mathrm{GL}(3)$
. Duke Math. J. 87(1997), 343–353. https://doi.org/10.1215/S0012-7094-97-08713-5
CrossRefGoogle Scholar
Blomer, V. and Brumley, F.,
On the Ramanujan conjecture over number fields
. Ann. of Math. (2) 174(2011), 581–605. https://doi.org/10.4007/annals.2011.174.1.18
CrossRefGoogle Scholar
Blomer, V., Fouvry, É., Kowalski, E., Michel, P., Milićević, D., and Sawin, W., The second moment theory of families of l-functions. Preprint, 2018. arxiv:1804.01450
Google Scholar
Bohr, H. and Jessen, B.,
Über die Werteverteilung der Riemannschen Zetafunktion
. Acta Math. 54(1930), 1–35. https://doi.org/10.1007/BF02547516
CrossRefGoogle Scholar
Bombieri, E. and Hejhal, D. A.,
On the distribution of zeros of linear combinations of Euler products
. Duke Math. J. 80(1995), 821–862. https://doi.org/10.1215/S0012-7094-95-08028-4
CrossRefGoogle Scholar
Bombieri, E. and Perelli, A.,
Distinct zeros of
 $L$
-functions
. Acta Arith. 83(1998), 271–281. https://doi.org/10.4064/aa-83-3-271-281
CrossRefGoogle Scholar
$L$
-functions
. Acta Arith. 83(1998), 271–281. https://doi.org/10.4064/aa-83-3-271-281
CrossRefGoogle Scholar
Bondarenko, A. and Seip, K.,
Large greatest common divisor sums and extreme values of the Riemann zeta function
. Duke Math. J. 166(2017), 1685–1701. https://doi.org/10.1215/00127094-0000005X
CrossRefGoogle Scholar
Bondarenko, A. and Seip, K.,
Extreme values of the Riemann zeta function and its argument
. Math. Ann. 372(2018), 999–1015. https://doi.org/10.1007/s00208-018-1663-2
CrossRefGoogle Scholar
Bondarenko, A. and Seip, K.,
Note on the resonance method for the Riemann zeta function
. In: 50 years with Hardy spaces, Oper. Theory Adv. Appl., 261, Birkhäuser/Springer,
Cham, 2018, pp. 121–139.CrossRefGoogle Scholar
Bordellès, O.,
Short interval results for certain arithmetic functions
. Int. J. Number Theory 14(2018), 535–548. https://doi.org/10.1142/S1793042118500331
CrossRefGoogle Scholar
Brumley, F.,
Effective multiplicity one on
 ${\mathrm{GL}}_N$
and narrow zero-free regions for Rankin-Selberg
${\mathrm{GL}}_N$
and narrow zero-free regions for Rankin-Selberg
 $L$
-functions
. Amer. J. Math. 128(2006), 1455–1474. http://muse.jhu.edu/journals/american_journal_of_mathematics/v128/128.6brumley.pdf
CrossRefGoogle Scholar
$L$
-functions
. Amer. J. Math. 128(2006), 1455–1474. http://muse.jhu.edu/journals/american_journal_of_mathematics/v128/128.6brumley.pdf
CrossRefGoogle Scholar
Chandee, V. and Soundararajan, K.,
Bounding
 $|\zeta \left(\frac{1}{2}+\mathrm{it}\right)|$
on the Riemann hypothesis
. Bull. Lond. Math. Soc. 43(2011), 243–250. https://doi.org/10.1112/blms/bdq095
CrossRefGoogle Scholar
$|\zeta \left(\frac{1}{2}+\mathrm{it}\right)|$
on the Riemann hypothesis
. Bull. Lond. Math. Soc. 43(2011), 243–250. https://doi.org/10.1112/blms/bdq095
CrossRefGoogle Scholar
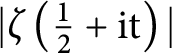 $|\zeta \left(\frac{1}{2}+\mathrm{it}\right)|$
on the Riemann hypothesis
. Bull. Lond. Math. Soc. 43(2011), 243–250. https://doi.org/10.1112/blms/bdq095
CrossRefGoogle Scholar
$|\zeta \left(\frac{1}{2}+\mathrm{it}\right)|$
on the Riemann hypothesis
. Bull. Lond. Math. Soc. 43(2011), 243–250. https://doi.org/10.1112/blms/bdq095
CrossRefGoogle ScholarConrey, J. B., Ghosh, A., and Gonek, S. M.,
Simple zeros of the zeta function of a quadratic number field. I. Invent Math. 86(1986), 563–576. https://doi.org/10.1007/BF01389269
CrossRefGoogle Scholar
Conrey, J. B., Ghosh, A., and Gonek, S. M.,
Simple zeros of the zeta-function of a quadratic number field
. II. In: Analytic number theory and Diophantine problems (Stillwater, OK, 1984), Progr. Math., 70, Birkhäuser Boston, Boston, MA, 1987, pp. 87–114.CrossRefGoogle Scholar
Conrey, J. B., Ghosh, A., and Gonek, S. M.,
Simple zeros of the Riemann zeta-function
. Proc. Lond. Math. Soc. (3) 76(1998), 497–522. https://doi.org/10.1112/S0024611598000306
CrossRefGoogle Scholar
Davenport, H.,
Multiplicative number theory
. 2nd ed., Graduate Texts in Mathematics, 74, Springer-Verlag,
New York-Berlin, 1980.Google Scholar
de la Bretèche, R. and Tenenbaum, G.,
Sommes de Gál et applications
. Proc. Lond. Math. Soc. (3) 119(2019), 104–134. https://doi.org/10.1112/plms.12224
CrossRefGoogle Scholar
Farmer, D. W., Gonek, S. M., and Hughes, C. P.,
The maximum size of
 $L$
-functions
. J. Reine Angew. Math. 609(2007), 215–236. https://doi.org/10.1515/CRELLE.2007.064
Google Scholar
$L$
-functions
. J. Reine Angew. Math. 609(2007), 215–236. https://doi.org/10.1515/CRELLE.2007.064
Google Scholar
Ford, K., Green, B., Konyagin, S., Maynard, J., and Tao, T.,
Long gaps between primes
. J. Amer. Math. Soc. 31(2018), 65–105. https://doi.org/10.1090/jams/876
CrossRefGoogle Scholar
Fujii, A.,
On the zeros of Dirichlet
 $L$
-functions
.
VII. Acta Arith. 29(1976), 59–68. https://doi.org/10.4064/aa-29-1-59-68
CrossRefGoogle Scholar
$L$
-functions
.
VII. Acta Arith. 29(1976), 59–68. https://doi.org/10.4064/aa-29-1-59-68
CrossRefGoogle Scholar
Fujii, A.,
Explicit formulas and oscillations
. In: Emerging applications of number theory (Minneapolis, MN, 1996), IMA Vol. Math. Appl., 109, Springer,
New York, 1999, pp. 219–267. https://doi.org/10.1007/978-1-4612-1544-8_9
CrossRefGoogle Scholar
Garunkštis, R. and Kalpokas, J.,
The discrete mean square of the Dirichlet
 $L$
-function at nontrivial zeros of another Dirichlet
$L$
-function at nontrivial zeros of another Dirichlet
 $L$
-function
. Int. J. Number Theory 9(2013), 945–963. https://doi.org/10.1142/S1793042113500085
CrossRefGoogle Scholar
$L$
-function
. Int. J. Number Theory 9(2013), 945–963. https://doi.org/10.1142/S1793042113500085
CrossRefGoogle Scholar
Godement, R. and Jacquet, H.,
Zeta functions of simple algebras
. Lecture Notes in Mathematics, 260, Springer-Verlag,
Berlin-New York, 1972.Google Scholar
Gonek, S. M.,
Mean values of the Riemann zeta function and its derivatives
. Invent. Math. 75(1984), 123–141. https://doi.org/10.1007/BF01403094
CrossRefGoogle Scholar
Hoffstein, J. and Ramakrishnan, D.,
Siegel zeros and cusp forms
. Internat. Math. Res. Notices 6(1995), 279–308. https://doi.org/10.1155/S1073792895000225
CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E.,
Analytic number theory
. American Mathematical Society Colloquium Publications, 53, American Mathematical Society,
Providence, RI, 2004. https://doi.org/10.1090/coll/053
Google Scholar
Jacquet, H. and Shalika, J. A.,
On Euler products and the classification of automorphic forms. II
. Amer. J. Math. 103(1981), 777–815. https://doi.org/10.2307/2374050
CrossRefGoogle Scholar
Jacquet, H. and Shalika, J. A.,
On Euler products and the classification of automorphic representations. I
. Amer. J. Math. 103(1981), 499–558. https://doi.org/10.2307/2374103
CrossRefGoogle Scholar
Kalpokas, J. and Šarka, P.,
Small values of the Riemann zeta function on the critical line
. Acta Arith. 169(2015), 201–220. https://doi.org/10.4064/aa169-3-1
CrossRefGoogle Scholar
Kim, H. and Sarnak, P.,
Refined estimates towards the Ramanujan and Selberg conjectures
. J. Amer. Math. Soc. 16(2003), 175–181.Google Scholar
Li, X. and Radziwiłł, M.,
The Riemann zeta function on vertical arithmetic progressions
. Int. Math. Res. Not. IMRN 2(2015), 325–354. https://doi.org/10.1093/imrn/rnt197
CrossRefGoogle Scholar
Littlewood, J. E.,
On the zeros of the Riemann zeta-function
. Math. Proc. Cambridge Philos. Soc. 22(1924), 295–318. http://dx.doi.org/10.1017/S0305004100014225
CrossRefGoogle Scholar
Liu, J. and Ye, Y.,
Perron’s formula and the prime number theorem for automorphic
 $L$
-functions
. Pure Appl. Math. Q. 3(2007), 481–497. https://doi.org/10.4310/PAMQ.2007.v3.n2.a4
CrossRefGoogle Scholar
$L$
-functions
. Pure Appl. Math. Q. 3(2007), 481–497. https://doi.org/10.4310/PAMQ.2007.v3.n2.a4
CrossRefGoogle Scholar
Luo, W., Rudnick, Z., and Sarnak, P., On the generalized Ramanujan conjecture for
 $GL(n)$
. In: Automorphic forms, automorphic representations, and arithmetic (Fort Worth, TX, 1996), Proc. Sympos. Pure Math., 66, Amer. Math. Soc., Providence, RI, 1999, pp. 301–310.CrossRefGoogle Scholar
$GL(n)$
. In: Automorphic forms, automorphic representations, and arithmetic (Fort Worth, TX, 1996), Proc. Sympos. Pure Math., 66, Amer. Math. Soc., Providence, RI, 1999, pp. 301–310.CrossRefGoogle Scholar
Montgomery, H. L.,
Extreme values of the Riemann zeta function
. Commentarii Mathematici Helvetici 52(1977), 511–518.CrossRefGoogle Scholar
Ng, N.,
A discrete mean value of the derivative of the Riemann zeta function
. Mathematika 54(2007), 113–155. https://doi.org/10.1112/S0025579300000255
CrossRefGoogle Scholar
Ng, N.,
Extreme values of
 ${\zeta}^{\prime}\left(\rho \right)$
. J. Lond. Math. Soc. (2) 78(2008), no. 2, 273–289. https://doi.org/10.1112/jlms/jdn022
CrossRefGoogle Scholar
${\zeta}^{\prime}\left(\rho \right)$
. J. Lond. Math. Soc. (2) 78(2008), no. 2, 273–289. https://doi.org/10.1112/jlms/jdn022
CrossRefGoogle Scholar
Raghunathan, R., A comparison of zeros of
 $L$
-functions. Math. Res. Lett. 6(1999), no. 2, 155–167. https://doi.org/10.4310/MRL.1999.v6.n2.a4
CrossRefGoogle Scholar
$L$
-functions. Math. Res. Lett. 6(1999), no. 2, 155–167. https://doi.org/10.4310/MRL.1999.v6.n2.a4
CrossRefGoogle Scholar
Selberg, A.,
Contributions to the theory of the Riemann zeta-function
. Arch. Math. Naturvid. 48(1946), 89–155.Google Scholar
Selberg, A., Old and new conjectures and results about a class of Dirichlet series. In: Proceedings of the Amalfi Conference on Analytic Number Theory (Maiori, 1989), Univ. Salerno, Salerno, 1992, pp. 367–385.Google Scholar
Soundararajan, K.,
Extreme values of zeta and
 $L$
-functions
. Math. Ann. 342(2008), 467–486. https://doi.org/10.1007/s00208-008-0243-2
CrossRefGoogle Scholar
$L$
-functions
. Math. Ann. 342(2008), 467–486. https://doi.org/10.1007/s00208-008-0243-2
CrossRefGoogle Scholar
Soundararajan, K. and Thorner, J.,
Weak subconvexity without a Ramanujan hypothesis.
With an appendix by Farrell Brumley. Duke Math. J. 168(2019), 1231–1268. https://doi.org/10.1215/00127094-2018-0065
CrossRefGoogle Scholar
Steuding, J., Value-distribution of
 $L$
-functions. Lecture Notes in Mathematics, 1877, Springer, Berlin, 2007.Google Scholar
$L$
-functions. Lecture Notes in Mathematics, 1877, Springer, Berlin, 2007.Google Scholar
Titchmarsh, E. C.,
The theory of the Riemann zeta-function
. Clarendon Press, Oxford, 1951.Google Scholar


