Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Harper, Malcolm
and
Murty, M. Ram
2004.
Euclidean Rings of Algebraic Integers.
Canadian Journal of Mathematics,
Vol. 56,
Issue. 1,
p.
71.
Narkiewicz, Władysław
2007.
Euclidean algorithm in small Abelian fields.
Functiones et Approximatio Commentarii Mathematici,
Vol. 37,
Issue. 2,
GRAVES, HESTER
2011.
$\mathbb{Q}(\sqrt{2}, \sqrt{35})$ HAS A NON-PRINCIPAL EUCLIDEAN IDEAL.
International Journal of Number Theory,
Vol. 07,
Issue. 08,
p.
2269.
Graves, Hester
and
Murty, M.
2013.
A family of number fields with unit rank at least 4 that has Euclidean ideals.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 9,
p.
2979.
Trifković, Mak
2013.
Algebraic Theory of Quadratic Numbers.
p.
87.
Chen, Ching-An
and
Leu, Ming-Guang
2013.
On a proposition of Samuel and 2-stage Euclidean algorithm in global fields.
Journal of Number Theory,
Vol. 133,
Issue. 1,
p.
215.
Glivický, Petr
and
Šaroch, Jan
2013.
Quasi-Euclidean subrings of ℚ[x].
Communications in Algebra,
Vol. 41,
Issue. 11,
p.
4267.
Graves, Hester
2013.
Growth results and Euclidean ideals.
Journal of Number Theory,
Vol. 133,
Issue. 8,
p.
2756.
Trifković, Mak
2013.
Algebraic Theory of Quadratic Numbers.
p.
131.
Long, D.D.
and
Thistlethwaite, Morwen B.
2016.
Lenstra–Hurwitz cliques and the class number one problem.
Journal of Number Theory,
Vol. 162,
Issue. ,
p.
564.
Chang, Wen-Yao
Cheng, Chih-Ren
and
Leu, Ming-Guang
2016.
A remark on the ring of algebraic integers in $$\mathbb{Q}(\sqrt { - d} )$$.
Israel Journal of Mathematics,
Vol. 216,
Issue. 2,
p.
605.
Hsu, Catherine
2016.
Two classes of number fields with a non-principal Euclidean ideal.
International Journal of Number Theory,
Vol. 12,
Issue. 04,
p.
1123.
Gun, Sanoli
and
Sivaraman, Jyothsnaa
2020.
On Existence of Euclidean Ideal Classes in Real Cubic and Quadratic Fields with Cyclic Class Group.
Michigan Mathematical Journal,
Vol. 69,
Issue. 2,
Srinivas, Kotyada
and
Subramani, Muthukrishnan
2020.
Class Groups of Number Fields and Related Topics.
p.
57.
Deshouillers, J.-M.
Gun, S.
and
Sivaraman, J.
2020.
On Euclidean ideal classes in certain Abelian extensions.
Mathematische Zeitschrift,
Vol. 296,
Issue. 1-2,
p.
847.
Lemmermeyer, Franz
2021.
Quadratic Number Fields.
p.
107.
Murty, V. Kumar
and
Sivaraman, J.
2022.
Euclidean ideal classes in Galois number fields of odd prime degree.
Research in Number Theory,
Vol. 8,
Issue. 3,
Sheydvasser, Arseniy (Senia)
2023.
Generating hyperbolic isometry groups by elementary matrices.
Communications in Algebra,
Vol. 51,
Issue. 8,
p.
3284.
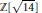 ] is Euclidean
] is Euclidean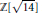 $\mathbb{Z}[\sqrt{14}]$ is a Euclidean domain. The proof is generalized to other real quadratic fields and to cyclotomic extensions of
$\mathbb{Z}[\sqrt{14}]$ is a Euclidean domain. The proof is generalized to other real quadratic fields and to cyclotomic extensions of 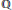 $\mathbb{Q}$ . It is proved that if
$\mathbb{Q}$ . It is proved that if  $K$ is a real quadratic field (modulo the existence of two special primes of
$K$ is a real quadratic field (modulo the existence of two special primes of  $K$ ) or if
$K$ ) or if  $K$ is a cyclotomic extension of
$K$ is a cyclotomic extension of 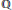 $\mathbb{Q}$ then:
$\mathbb{Q}$ then: $K$ is a Euclidean domain if and only if it is a principal ideal domain.
$K$ is a Euclidean domain if and only if it is a principal ideal domain. $K$ is a totally real extension of degree at least three. The main changes are a new Motzkin-type lemma and the addition of the large sieve to the argument. These changes allow application of a powerful theorem due to Bombieri, Friedlander and Iwaniec in order to obtain the result in the real quadratic case. The modification also allows the completion of the classification of cyclotomic extensions in terms of the Euclidean property.
$K$ is a totally real extension of degree at least three. The main changes are a new Motzkin-type lemma and the addition of the large sieve to the argument. These changes allow application of a powerful theorem due to Bombieri, Friedlander and Iwaniec in order to obtain the result in the real quadratic case. The modification also allows the completion of the classification of cyclotomic extensions in terms of the Euclidean property.
