No CrossRef data available.
Article contents
Invertibility Threshold for Nevanlinna Quotient Algebras
Published online by Cambridge University Press: 10 September 2021
Abstract
Let 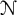 $\mathcal {N}$ be the Nevanlinna class, and let B be a Blaschke product. It is shown that the natural invertibility criterion in the quotient algebra
$\mathcal {N}$ be the Nevanlinna class, and let B be a Blaschke product. It is shown that the natural invertibility criterion in the quotient algebra 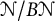 $\mathcal {N} / B \mathcal {N}$, that is,
$\mathcal {N} / B \mathcal {N}$, that is, 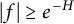 $|f| \ge e^{-H} $ on the set
$|f| \ge e^{-H} $ on the set 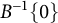 $B^{-1}\{0\}$ for some positive harmonic function H, holds if and only if the function
$B^{-1}\{0\}$ for some positive harmonic function H, holds if and only if the function 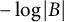 $- \log |B|$ has a harmonic majorant on the set
$- \log |B|$ has a harmonic majorant on the set 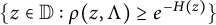 $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$, at least for large enough functions H. We also study the corresponding class of positive harmonic functions H on the unit disc such that the latter condition holds. We also discuss the analogous invertibility problem in quotients of the Smirnov class.
$\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$, at least for large enough functions H. We also study the corresponding class of positive harmonic functions H on the unit disc such that the latter condition holds. We also discuss the analogous invertibility problem in quotients of the Smirnov class.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
First author is supported by the Generalitat de Catalunya (grant 2017 SGR 395) and the Spanish Ministerio de Ciencia e Innovación (project MTM2017-85666-P).


