Article contents
Induced Coactions of Discrete Groups on C *-Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
Using the close relationship between coactions of discrete groups and Fell bundles, we introduce a procedure for inducing a 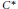 ${{C}^{*}}$ -coaction
${{C}^{*}}$ -coaction 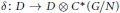 $\delta :D\to D\otimes {{C}^{*}}\left( G/N \right)$ of a quotient group
$\delta :D\to D\otimes {{C}^{*}}\left( G/N \right)$ of a quotient group 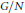 $G/N$ of a discrete group
$G/N$ of a discrete group 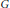 $G$ to a
$G$ to a 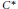 ${{C}^{*}}$ -coaction
${{C}^{*}}$ -coaction 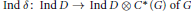 $\text{Ind}\,\delta \text{:}\,\text{Ind}\,D\to \text{Ind}\,D\otimes {{C}^{*}}\left( G \right)\,\text{of }G$ . We show that induced coactions behave in many respects similarly to induced actions. In particular, as an analogue of the well known imprimitivity theorem for induced actions we prove that the crossed products
$\text{Ind}\,\delta \text{:}\,\text{Ind}\,D\to \text{Ind}\,D\otimes {{C}^{*}}\left( G \right)\,\text{of }G$ . We show that induced coactions behave in many respects similarly to induced actions. In particular, as an analogue of the well known imprimitivity theorem for induced actions we prove that the crossed products 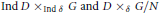 $\text{Ind}\,D{{\times }_{\text{Ind}\,\delta }}\,G\,\text{and }D{{\times }_{\delta }}\,G/N$ are always Morita equivalent. We also obtain nonabelian analogues of a theorem of Olesen and Pedersen which show that there is a duality between induced coactions and twisted actions in the sense of Green. We further investigate amenability of Fell bundles corresponding to induced coactions.
$\text{Ind}\,D{{\times }_{\text{Ind}\,\delta }}\,G\,\text{and }D{{\times }_{\delta }}\,G/N$ are always Morita equivalent. We also obtain nonabelian analogues of a theorem of Olesen and Pedersen which show that there is a duality between induced coactions and twisted actions in the sense of Green. We further investigate amenability of Fell bundles corresponding to induced coactions.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
- 7
- Cited by

