No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Cubical sets and their homology have been used in dynamical systems as well as in digital imaging. We take a fresh look at this topic, following Zariski ideas from algebraic geometry. The cubical topology is defined to be a topology in 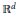 ${{\mathbb{R}}^{d}}$ in which a set is closed if and only if it is cubical. This concept is a convenient frame for describing a variety of important features of cubical sets. Separation axioms which, in general, are not satisfied here, characterize exactly those pairs of points which we want to distinguish. The noetherian property guarantees the correctness of the algorithms. Moreover, maps between cubical sets which are continuous and closed with respect to the cubical topology are precisely those for whom the homology map can be defined and computed without grid subdivisions. A combinatorial version of the Vietoris–Begle theorem is derived. This theorem plays the central role in an algorithm computing homology of maps which are continuous with respect to the Euclidean topology.
${{\mathbb{R}}^{d}}$ in which a set is closed if and only if it is cubical. This concept is a convenient frame for describing a variety of important features of cubical sets. Separation axioms which, in general, are not satisfied here, characterize exactly those pairs of points which we want to distinguish. The noetherian property guarantees the correctness of the algorithms. Moreover, maps between cubical sets which are continuous and closed with respect to the cubical topology are precisely those for whom the homology map can be defined and computed without grid subdivisions. A combinatorial version of the Vietoris–Begle theorem is derived. This theorem plays the central role in an algorithm computing homology of maps which are continuous with respect to the Euclidean topology.