Published online by Cambridge University Press: 20 November 2018
We give a description of the monoid of Murray-von Neumann equivalence classes of projections for multiplier algebras of a wide class of 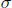 $\sigma $-unital simple
$\sigma $-unital simple 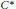 ${{C}^{*}}$-algebras
${{C}^{*}}$-algebras  $A$ with real rank zero and stable rank one. The lattice of ideals of this monoid, which is known to be crucial for understanding the ideal structure of the multiplier algebra
$A$ with real rank zero and stable rank one. The lattice of ideals of this monoid, which is known to be crucial for understanding the ideal structure of the multiplier algebra 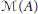 $\mathcal{M}(A)$, is therefore analyzed. In important cases it is shown that, if
$\mathcal{M}(A)$, is therefore analyzed. In important cases it is shown that, if  $A$ has finite scale then the quotient of
$A$ has finite scale then the quotient of 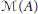 $\mathcal{M}(A)$ modulo any closed ideal
$\mathcal{M}(A)$ modulo any closed ideal 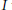 $I$ that properly contains
$I$ that properly contains  $A$ has stable rank one. The intricacy of the ideal structure of
$A$ has stable rank one. The intricacy of the ideal structure of 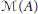 $\mathcal{M}(A)$ is reflected in the fact that
$\mathcal{M}(A)$ is reflected in the fact that 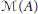 $\mathcal{M}(A)$ can have uncountably many different quotients, each one having uncountably many closed ideals forming a chain with respect to inclusion.
$\mathcal{M}(A)$ can have uncountably many different quotients, each one having uncountably many closed ideals forming a chain with respect to inclusion.