Hostname: page-component-857557d7f7-nbs69 Total loading time: 0 Render date: 2025-11-23T19:21:11.504Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hopf Ring for P(n)

Published online by Cambridge University Press:  20 November 2018

Douglas C. Ravenel  and
W. Stephen Wilson
Douglas C. Ravenel
Affiliation:
University of Rochester Rochester, New York 14627 U.S.A. email: drav@troi.cc.rochester.edu
W. Stephen Wilson
Affiliation:
Johns Hopkins University Baltimore, Maryland 21218 U.S.A. email: email:wsw@math.jhu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

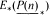We show that , the E-homology of the Ω-spectrum for P(n), is an E* free Hopf ring for E a complex oriented theory with I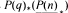n sent to 0. This covers the cases and 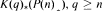. The generators of the Hopf ring are those necessary for the stable result. The motivation for this paper is to show that P(n) satisfies all of the conditions for the machinery of unstable cohomology operations set up in [BJW95]. This can then be used to produce splittings analogous to those for BP done in [Wil75]

Keywords

55N2255N20

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 5 , 01 October 1996 , pp. 1044 - 1063
Copyright
Copyright © Canadian Mathematical Society 1996

References

[Baa73] Baas, N.A., On bordism theory of manifolds with singularities, Math., Scand. 33(1973), 279–302.Google Scholar
[BJW95] Boardman, J.M., Johnson, D.C., and Wilson, W.S., Unstable operations in generalized cohomology. In: The Handbook of Algebraic Topology, (ed. James, I.M.), Chapter 15, Elsevier, 1995. 687–822.Google Scholar
[BM71] Baas, N.A. and Madsen, I., On the realization of certain modules over the Steenrod algebra, Math., Scand. 31(1971), 220–224.Google Scholar
[Boa95] Boardman, J.M., Stable operations in generalized cohomology, In: The Handbook of Algebraic Topology, (ed. James, I.M.), Chapter 14, Elsevier, 1995. 585–686.Google Scholar
[BW] Boardman, J.M. and Wilson, W.S., k(n)-torsion-free H-spaces and P(n)-cohomology, preprint.Google Scholar
[ETW] Eccles, P.J., Turner, P.R., and Wilson, W.S., On the Hopfring for the sphere, Math. Z., to appear.Google Scholar
[Har9] Hara, J S., The Hopfrings for connective Morava K-theory and connective complex K-theory, J. Math. Kyoto Univ., (1) 31(1991), 43–70.Google Scholar
[HRW] Hopkins, M.J., Ravenel, D.C., and Wilson, W.S., Morava Hopf algebras and spaces K(n) equivalent to finite Postnikov systems, submitted.Google Scholar
[JW75] Johnson, D.C. and Wilson, W.S., BP-operations and Morava s extraordinary K-theories, Math., Z. 144(1975), 55–75.Google Scholar
[Kra90] Kramer, R., The periodic Hopf ring of connective Morava K-theory, PhD thesis, Johns Hopkins University, 1990.Google Scholar
[Mor79J Morava, J., A product for odd-primary bordism of manifolds with singularities,, Topology 18(1979), 177–186.Google Scholar
[RW77] Ravenel, D.C. and Wilson, W.S., The Hopf ring for complex cobordism, J. Pure Appl., Algebra 9(1977), 241–280.Google Scholar
[RW80] Ravenel, D.C., The Morava K-theories of Eilenberg-MacLane spaces and the Conner-Floyd conjecture, Amer. J., Math. 102(1980), 691–748.Google Scholar
[Str92] Strickland, N., Bott periodicity and Hopf rings, PhD thesis, University of Manchester, 1992.Google Scholar
[SY76] Shimada, N. and Yagita, N., Multiplications in complex bordism theory with singularities, Publ. Res. Inst. Math. Sci., Kyoto, Univ. 12(1976), 259–293.Google Scholar
[Tur] Turner, P.R., Dickson coinvariants and the homology ofH*QSP, Math. Z., to appear.Google Scholar
[TW80] Thomason, R.W. and Wilson, W.S., Hopf rings in the bar spectral sequence, Quart. J., Math. 31(1980), 507–511.Google Scholar
[WH751 Wilson, W.S., The Ω-spectrum for Brown-Peterson cohomology, Part II, Amer. J., Math. 97(1975), 101–123.Google Scholar
[WH82] Wilson, W.S., Brown-Peterson homology: an introduction and sampler. In: C. B. M. S. Regional Conference Series Math. 48, Amer. Math. Soc, Providence, Rhode Island, 1982.Google Scholar
[WH84] Wilson, W.S., The Hopf ring for Morava K-theory, Publ. Res. Inst. Math. Sci., Kyoto, Univ. 20(1984), 1025–1036.Google Scholar
[Wür77] Würgler, U., On products in a family of cohomology theories associated to the invariant prime ideals Of π*(BP), Comment. Math., Helv. 52(1977), 457–481.Google Scholar
[Yag77] Yagita, N., On the algebraic structure of cobordism operations with singularities, J. London Math., Soc. 16(1977), 131–141.Google Scholar