Article contents
Homology TQFT's and the Alexander–Reidemeister Invariant of 3-Manifolds via Hopf Algebras and Skein Theory
Published online by Cambridge University Press: 20 November 2018
Abstract
We develop an explicit skein-theoretical algorithm to compute the Alexander polynomial of a 3-manifold from a surgery presentation employing the methods used in the construction of quantum invariants of 3-manifolds. As a prerequisite we establish and prove a rather unexpected equivalence between the topological quantum field theory constructed by Frohman and Nicas using the homology of 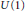 $U\left( 1 \right)$ -representation varieties on the one side and the combinatorially constructed Hennings TQFT based on the quasitriangular Hopf algebra
$U\left( 1 \right)$ -representation varieties on the one side and the combinatorially constructed Hennings TQFT based on the quasitriangular Hopf algebra 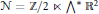 $\mathcal{N=}\mathbb{Z}\text{/2}\ltimes {{\wedge }^{*}}{{\mathbb{R}}^{2}}$ on the other side. We find that both TQFT's are
$\mathcal{N=}\mathbb{Z}\text{/2}\ltimes {{\wedge }^{*}}{{\mathbb{R}}^{2}}$ on the other side. We find that both TQFT's are 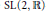 $\text{SL}\left( 2,\,\mathbb{R} \right)$ -equivariant functors and, as such, are isomorphic. The
$\text{SL}\left( 2,\,\mathbb{R} \right)$ -equivariant functors and, as such, are isomorphic. The 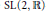 $\text{SL}\left( 2,\,\mathbb{R} \right)$ -action in the Hennings construction comes from the natural action on
$\text{SL}\left( 2,\,\mathbb{R} \right)$ -action in the Hennings construction comes from the natural action on 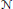 $\mathcal{N}$ and in the case of the Frohman–Nicas theory from the Hard–Lefschetz decomposition of the
$\mathcal{N}$ and in the case of the Frohman–Nicas theory from the Hard–Lefschetz decomposition of the 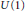 $U\left( 1 \right)$ -moduli spaces given that they are naturally Kähler. The irreducible components of this TQFT, corresponding to simple representations of
$U\left( 1 \right)$ -moduli spaces given that they are naturally Kähler. The irreducible components of this TQFT, corresponding to simple representations of 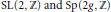 $\text{SL}\left( 2,\,\mathbb{Z} \right)\,\text{and}\,\text{Sp}\left( 2g,\,\mathbb{Z} \right)$ , thus yield a large family of homological TQFT's by taking sums and products. We give several examples of TQFT's and invariants that appear to fit into this family, such as Milnor and Reidemeister Torsion, Seiberg–Witten theories, Casson type theories for homology circles à la Donaldson, higher rank gauge theories following Frohman and Nicas, and the
$\text{SL}\left( 2,\,\mathbb{Z} \right)\,\text{and}\,\text{Sp}\left( 2g,\,\mathbb{Z} \right)$ , thus yield a large family of homological TQFT's by taking sums and products. We give several examples of TQFT's and invariants that appear to fit into this family, such as Milnor and Reidemeister Torsion, Seiberg–Witten theories, Casson type theories for homology circles à la Donaldson, higher rank gauge theories following Frohman and Nicas, and the 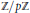 $\mathbb{Z}/p\mathbb{Z}$ reductions of Reshetikhin–Turaev theories over the cyclotomic integers
$\mathbb{Z}/p\mathbb{Z}$ reductions of Reshetikhin–Turaev theories over the cyclotomic integers 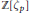 $\mathbb{Z}[{{\zeta }_{p}}]$ . We also conjecture that the Hennings TQFT for quantum-
$\mathbb{Z}[{{\zeta }_{p}}]$ . We also conjecture that the Hennings TQFT for quantum- 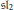 $\mathfrak{s}{{\mathfrak{l}}_{2}}$ is the product of the Reshetikhin–Turaev TQFT and such a homological TQFT.
$\mathfrak{s}{{\mathfrak{l}}_{2}}$ is the product of the Reshetikhin–Turaev TQFT and such a homological TQFT.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
- 15
- Cited by

