No CrossRef data available.
Article contents
The Homology of Abelian Covers of Knotted Graphs
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 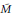 $\tilde{M}$ be a regular branched cover of a homology 3-sphere
$\tilde{M}$ be a regular branched cover of a homology 3-sphere 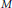 $M$ with deck group
$M$ with deck group 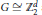 $G\cong \mathbb{Z}_{2}^{d}$ and branch set a trivalent graph
$G\cong \mathbb{Z}_{2}^{d}$ and branch set a trivalent graph  $\Gamma $ ; such a cover is determined by a coloring of the edges of
$\Gamma $ ; such a cover is determined by a coloring of the edges of  $\Gamma $ with elements of
$\Gamma $ with elements of  $G$ . For each index-2 subgroup
$G$ . For each index-2 subgroup 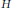 $H$ of
$H$ of 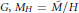 $G,\,{{M}_{H}}=\tilde{M}/H$ is a double branched cover of
$G,\,{{M}_{H}}=\tilde{M}/H$ is a double branched cover of 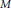 $M$ . Sakuma has proved that
$M$ . Sakuma has proved that 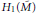 ${{H}_{1}}\left( {\tilde{M}} \right)$ is isomorphic, modulo 2-torsion, to
${{H}_{1}}\left( {\tilde{M}} \right)$ is isomorphic, modulo 2-torsion, to 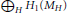 ${{\oplus }_{H}}{{H}_{1}}\left( {{M}_{H}} \right)$ , and has shown that
${{\oplus }_{H}}{{H}_{1}}\left( {{M}_{H}} \right)$ , and has shown that 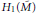 ${{H}_{1}}\left( {\tilde{M}} \right)$ is determined up to isomorphism by
${{H}_{1}}\left( {\tilde{M}} \right)$ is determined up to isomorphism by 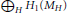 ${{\oplus }_{H}}{{H}_{1}}\left( {{M}_{H}} \right)$ in certain cases; specifically, when
${{\oplus }_{H}}{{H}_{1}}\left( {{M}_{H}} \right)$ in certain cases; specifically, when 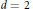 $d=2$ and the coloring is such that the branch set of each cover
$d=2$ and the coloring is such that the branch set of each cover 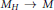 ${{M}_{H}}\to M$ is connected, and when
${{M}_{H}}\to M$ is connected, and when  $d=3$ and
$d=3$ and  $\Gamma $ is the complete graph
$\Gamma $ is the complete graph 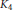 ${{K}_{4}}$ . We prove this for a larger class of coverings: when
${{K}_{4}}$ . We prove this for a larger class of coverings: when 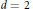 $d=2$ , for any coloring of a connected graph; when
$d=2$ , for any coloring of a connected graph; when 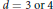 $d=3\,\text{or}\,\text{4}$ , for an infinite class of colored graphs; and when
$d=3\,\text{or}\,\text{4}$ , for an infinite class of colored graphs; and when 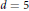 $d=5$ , for a single coloring of the Petersen graph.
$d=5$ , for a single coloring of the Petersen graph.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999

