Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Litherland, R. A.
1999.
The Homology of Abelian Covers of Knotted Graphs.
Canadian Journal of Mathematics,
Vol. 51,
Issue. 5,
p.
1035.
TAYAMA, IKUO
2000.
FIRST BETTI NUMBERS OF ABELIAN COVERINGS OF THE COMPLEX PROJECTIVE PLANE BRANCHED OVER LINE CONFIGURATIONS.
Journal of Knot Theory and Its Ramifications,
Vol. 09,
Issue. 02,
p.
271.
Libgober, A.
2001.
Applications of Algebraic Geometry to Coding Theory, Physics and Computation.
p.
215.
Morishita, Masanori
2001.
A theory of genera for cyclic coverings of links.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 77,
Issue. 7,
Mednykh, Alexander
and
Reni, Marco
2001.
Twofold unbranched coverings of genus two 3-manifolds are hyperelliptic.
Israel Journal of Mathematics,
Vol. 123,
Issue. 1,
p.
149.
Mecchia, Mattia
and
Reni, Marco
2002.
Hyperbolic 2-fold branched coverings of links and their quotients.
Pacific Journal of Mathematics,
Vol. 202,
Issue. 2,
p.
429.
Suciu, Alexander I.
2002.
Translated tori in the characteristic varieties of complex hyperplane arrangements.
Topology and its Applications,
Vol. 118,
Issue. 1-2,
p.
209.
Silver, Daniel S.
and
Williams, Susan G.
2002.
Mahler measure, links and homology growth.
Topology,
Vol. 41,
Issue. 5,
p.
979.
Cohen, Daniel C.
and
Orlik, Peter
2002.
Some cyclic covers of complements of arrangements.
Topology and its Applications,
Vol. 118,
Issue. 1-2,
p.
3.
Song, Hyun Jong
2003.
Morimoto–Sakuma–Yokota's geometric approach to tunnel number one knots.
Topology and its Applications,
Vol. 127,
Issue. 3,
p.
375.
Cohen, Daniel C
Denham, Graham
and
Suciu, Alexander I
2003.
Torsion in Milnor fiber homology.
Algebraic & Geometric Topology,
Vol. 3,
Issue. 1,
p.
511.
Budur, Nero
2009.
Unitary local systems, multiplier ideals, and polynomial periodicity of Hodge numbers.
Advances in Mathematics,
Vol. 221,
Issue. 1,
p.
217.
Bartolo, Enrique Artal
Cogolludo-Agustín, Jose Ignacio
and
Libgober, Anatoly
2012.
Configuration Spaces.
p.
81.
Artal Bartolo, Enrique
2014.
Topology of arrangements and position of singularities.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 23,
Issue. 2,
p.
223.
Suciu, Alexander I.
2014.
Hyperplane arrangements and Milnor fibrations.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 23,
Issue. 2,
p.
417.
FRIEDL, STEFAN
and
POWELL, MARK
2014.
Links not concordant to the Hopf link.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 156,
Issue. 3,
p.
425.
Mecchia, Mattia
2020.
Finite groups acting on hyperelliptic 3-manifolds.
Journal of Knot Theory and Its Ramifications,
Vol. 29,
Issue. 04,
p.
2050021.
Sakuma, Makoto
2020.
In the Tradition of Thurston.
p.
67.
Yoshinaga, Masahiko
2020.
Double coverings of arrangement complements and 2-torsion in Milnor fiber homology.
European Journal of Mathematics,
Vol. 6,
Issue. 3,
p.
1097.
Mednykh, A. D.
and
Mednykh, I. A.
2021.
Plans’ Periodicity Theorem for Jacobian of Circulant Graphs.
Doklady Mathematics,
Vol. 103,
Issue. 3,
p.
139.

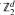 -coverings of spatial graphs. As an application, we generalize a result of E. Hironaka on polynomial periodicity of the first Betti numbers in certain towers of abelian coverings of complex surfaces.
-coverings of spatial graphs. As an application, we generalize a result of E. Hironaka on polynomial periodicity of the first Betti numbers in certain towers of abelian coverings of complex surfaces.