Hostname: page-component-cb9f654ff-mx8w7 Total loading time: 0 Render date: 2025-09-02T15:43:41.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Homological Aspects of Semigroup Gradings on Rings and Algebras

Published online by Cambridge University Press:  20 November 2018

W. D. Burgess  and
Manuel Saorín
W. D. Burgess
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, Ottawa, Ontario, K1N 6N5 email: wdbsg@uottawa.ca
Manuel Saorín
Affiliation:
Departemento de Matemáticas, Universidad de Murcia, 30100 Espinardo, Murcia, Spain email: msaorinc@fcu.um.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This article studies algebras $R$ over a simple artinian ring 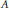$A$ , presented by a quiver and relations and graded by a semigroup $\Sigma $ . Suitable semigroups often arise from a presentation of $R$ . Throughout, the algebras need not be finite dimensional. The graded 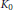${{K}_{0}}$ , along with the $\Sigma $ -graded Cartan endomorphisms and Cartan matrices, is examined. It is used to study homological properties.

A test is found for finiteness of the global dimension of a monomial algebra in terms of the invertibility of the Hilbert $\Sigma $ -series in the associated path incidence ring.

The rationality of the $\Sigma $ -Euler characteristic, the Hilbert $\Sigma $ -series and the Poincaré-Betti $\Sigma $ -series is studied when $\Sigma $ is torsion-free commutative and 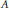$A$ is a division ring. These results are then applied to the classical series. Finally, we find new finite dimensional algebras for which the strong no loops conjecture holds.

Keywords

16W5016E2016G20

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 488 - 505
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Anick, D., Recent progress in Hilbert and Poincaré series. In: Algebraic Topology—Rational Homotopy (ed. Félix, Y.), Lecture Notes in Math. 1318, Springer-Verlag, New York-Heidelberg, 1988, 1–25.Google Scholar
[2] Anick, D., On the homology of associative algebras. Trans. Amer.Math. Soc. 296 (1986), 641–659.Google Scholar
[3] Anick, D. J. and Green, E. L., On the homology of quotients of path algebras. Comm. Algebra 15 (1987), 309–341.Google Scholar
[4] Backelin, J., La série de Poincaré-Betti d’une algèbre graduée de type fini à une relation est rationnelle. C. R. Acad. Sci. Paris 287 (1978), 843–846.Google Scholar
[5] Burgess, W. D., The graded Cartan matrix and global dimension of 0-relations algebras. Proc. Edinburgh Math. Soc. 30 (1987), 351–362.Google Scholar
[6] Butler, M. C. R., The syzygy theorem for monomial algebras. Typescript, 1997.Google Scholar
[7] Cibils, C., The syzygy quiver and the finitistic dimension. Comm. Algebra 21 (1993), 4167–4171.Google Scholar
[8] Content, M., Lemay, F. and Leroux, P., Catégories de Möbius et fonctorialités : un cadre général pour l’inversion de Möbius. J. Combin. Theory Ser. A 28 (1980), 169–190.Google Scholar
[9] Farkas, D. R., The Anick resolution. J. Pure Appl. Algebra 79 (1992), 159–168.Google Scholar
[10] Farkas, D. R., Feustel, C. D. and Green, E. L., Synergy in the theories of Gröbner bases and path algebras. Canad. J. Math. 45 (1993), 727–739.Google Scholar
[11] Gilmer, R., Commutative semigroup rings. Univ. Chicago Press, Chicago, 1984.Google Scholar
[12] Govorov, V. E., Dimension and multiplicity of graded algebras. Siberian Math. J. 14 (1973), 840–845.Google Scholar
[13] Green, E. and Huang, R. Q., Projective resolutions of straightening closed algebras generated by minors. Adv. in Math. 110 (1995), 314–333.Google Scholar
[14] Huisgen, B. Z., Field-dependent homological behavior of finite dimensional algebras. Manuscripta Math. 82 (1994), 15–29.Google Scholar
[15] Igusa, K., Notes on the no loops conjecture. J. Pure Appl. Algebra. 69 (1990), 161–176.Google Scholar
[16] Leroux, P. and Sarraillé, J., Structure of incidence algebras of graphs. Comm. Algebra 9 (1981), 1479–1517.Google Scholar
[17] Nastasescu, C. and Van Oystaeyen, F., Graded Ring Theory. North Holland Math. Libr. 28, Amsterdam-New York-Oxford, 1982.Google Scholar
[18] Roy, A., A note on filtered rings. Arch. Math. 16 (1965), 421–427.Google Scholar
[19] Saorín, M., Monoid gradings on algebras and the Cartan determinant conjecture. Proc. EdinburghMath. Soc., to appear.Google Scholar
[20] Stephenson, D. R., Artin-Schelter regular algebras of global dimension three. J. Algebra 183 (1996), 55–73.Google Scholar
[21] Vasconcelos, W. V., The rings of dimension two. Lecture Notes in Pure Appl. Math. 22, Marcel Dekker, New York, 1976.Google Scholar