No CrossRef data available.
Article contents
High Level Occupation Times for Gaussian Stochastic Processes with Sample Paths in Orlicz Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let X be a complete separable metric space, and 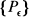 a family of probability measures on the Borel subsets of X. We say that
a family of probability measures on the Borel subsets of X. We say that 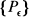 obeys the large deviation principle (LDP) with a rate function I(·) if there exists a function I(·) from X into [0, ∞] satisfying:
obeys the large deviation principle (LDP) with a rate function I(·) if there exists a function I(·) from X into [0, ∞] satisfying:
-
(i) 0 ≦ I(x) ≦ ∞ for all x ∊ X.
-
(ii) I(·) is lower semicontinuous.
-
(iii) For each l < ∞ the set {x:I(x) ≦ l} is a compact set in X.
-
(iv) For each closed set C ⊂ X
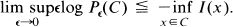
-
(v) For each open set C ⊂ X
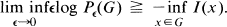
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1987
References
1.
Byczkowski, T., Gaussian measures on Lp spaces, 0 < p < ∞, Studia Math.
59 (1977), 249–261.Google Scholar
2.
Byczkowski, T., Norm convergent expansion for Lϕ-valued Gaussian random elements, Studia Math.
64(1979), 87–95.Google Scholar
3.
Donsker, M.D. and Varadhan, S.R.S., Asymptotic evaluation of certain Markov processes expectations for large time — III, Comm. Pure Appl. Math.
29 (1976), 389–461.Google Scholar
5.
Hille, E. and Phillips, R., Functional analysis and semigroups, AMS Colloquium Publications,
31 (1975).Google Scholar
6.
Kallianpur, G. and Oodaira, H., Freidlin-Wentzell type estimates for abstract Wiener spaces, Sankhyà
40, Series A (1978), 116–137.Google Scholar
7.
Lawniczak, A.T., Gaussian measures on Orlicz spaces and abstract Wiener spaces, Lecture Notes in Mathematics
939 (Springer-Verlag, 1982), 81–97.Google Scholar
8.
Lawniczak, A.T., Gaussian measures on Orlicz spaces, Stoch. Analysis and its Appl.
3 (1985).Google Scholar
9.
Marlow, N., High level occupation times for continuous Gaussian processes, Ann. of Probab.
3 (1973), 388–397.Google Scholar
11.
Strook, D.W., An introduction to the theory of large deviations, (Springer-Verlag, 1984).CrossRefGoogle Scholar

