Article contents
The Heat Equation on the Spaces of Positive Definite Matrices
Published online by Cambridge University Press: 20 November 2018
Abstract
The main topic of this paper is the study of the fundamental solution of the heat equation for the symmetric spaces of positive definite matrices, Pos(n,R).
Our first step is to develop a “False Abel Inverse Transform”  which transforms functions of compact support on an euclidean space into integrable functions on the symmetric space. The transform
which transforms functions of compact support on an euclidean space into integrable functions on the symmetric space. The transform  is shown to satisfy the relation
is shown to satisfy the relation 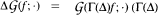 is the usual Laplacian with a constant drift).
is the usual Laplacian with a constant drift).
Using this transform, we find explicit formulas for the heat kernel in the cases n = 2 and n = 3. These formulas allow us to give the asymptotic development for the heat kernel as t tends to infinity. Finally, we give an upper and lower bound of the same type for the heat kernel.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1992
References
- 9
- Cited by

