Article contents
The Geometry of 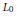 ${{L}_{0}}$
${{L}_{0}}$
Published online by Cambridge University Press: 20 November 2018
Abstract
Suppose that we have the unit Euclidean ball in 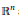 ${{\mathbb{R}}^{n}}$ and construct new bodies using three operations — linear transformations, closure in the radial metric, and multiplicative summation defined by
${{\mathbb{R}}^{n}}$ and construct new bodies using three operations — linear transformations, closure in the radial metric, and multiplicative summation defined by  ${{\left\| x \right\|}_{K+0L}}\,=\,\sqrt{{{\left\| x \right\|}_{K}}{{\left\| x \right\|}_{L}}}$ . We prove that in dimension 3 this procedure gives all origin-symmetric convex bodies, while this is no longer true in dimensions 4 and higher. We introduce the concept of embedding of a normed space in
${{\left\| x \right\|}_{K+0L}}\,=\,\sqrt{{{\left\| x \right\|}_{K}}{{\left\| x \right\|}_{L}}}$ . We prove that in dimension 3 this procedure gives all origin-symmetric convex bodies, while this is no longer true in dimensions 4 and higher. We introduce the concept of embedding of a normed space in 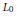 ${{L}_{0}}$ that naturally extends the corresponding properties of
${{L}_{0}}$ that naturally extends the corresponding properties of 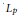 ${{L}_{P}}$ -spaces with
${{L}_{P}}$ -spaces with 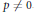 $p\,\ne \,0$ , and show that the procedure described above gives exactly the unit balls of subspaces of
$p\,\ne \,0$ , and show that the procedure described above gives exactly the unit balls of subspaces of 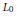 ${{L}_{0}}$ in every dimension. We provide Fourier analytic and geometric characterizations of spaces embedding in
${{L}_{0}}$ in every dimension. We provide Fourier analytic and geometric characterizations of spaces embedding in 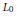 ${{L}_{0}}$ , and prove several facts confirming the place of
${{L}_{0}}$ , and prove several facts confirming the place of 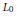 ${{L}_{0}}$ in the scale of
${{L}_{0}}$ in the scale of 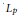 ${{L}_{P}}$ -spaces.
${{L}_{P}}$ -spaces.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 15
- Cited by

