Article contents
Generalized Polynomials and Mild Mixing
Published online by Cambridge University Press: 20 November 2018
Abstract
An unsettled conjecture of V. Bergelson and I. Håland proposes that if 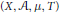 $(X,\,\mathcal{A},\,\mu ,\,T)$ is an invertible weak mixing measure preserving system, where
$(X,\,\mathcal{A},\,\mu ,\,T)$ is an invertible weak mixing measure preserving system, where 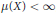 $\mu (X)<\infty $ , and if
$\mu (X)<\infty $ , and if 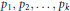 ${{p}_{1}},{{p}_{2}},...,{{p}_{k}}$ are generalized polynomials (functions built out of regular polynomials via iterated use of the greatest integer or floor function) having the property that no
${{p}_{1}},{{p}_{2}},...,{{p}_{k}}$ are generalized polynomials (functions built out of regular polynomials via iterated use of the greatest integer or floor function) having the property that no 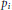 ${{p}_{i}}$ , nor any
${{p}_{i}}$ , nor any 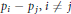 ${{p}_{i}}-{{p}_{j,}}i\ne j$ , is constant on a set of positive density, then for any measurable sets
${{p}_{i}}-{{p}_{j,}}i\ne j$ , is constant on a set of positive density, then for any measurable sets 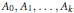 ${{A}_{0}},{{A}_{1}},...,{{A}_{K}}$ , there exists a zero-density set
${{A}_{0}},{{A}_{1}},...,{{A}_{K}}$ , there exists a zero-density set 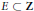 $E\subset Z$ such that
$E\subset Z$ such that
1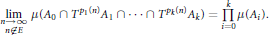 $$\underset{n\notin E}{\mathop{\underset{n\to \infty }{\mathop{\lim }}\,}}\,\mu ({{A}_{0}}\cap {{T}^{p1(n)}}{{A}_{1}}\cap \ldots \cap {{T}^{pk(n)}}{{A}_{k}})=\prod\limits_{i=0}^{k}{\mu ({{A}_{i}}).}$$
$$\underset{n\notin E}{\mathop{\underset{n\to \infty }{\mathop{\lim }}\,}}\,\mu ({{A}_{0}}\cap {{T}^{p1(n)}}{{A}_{1}}\cap \ldots \cap {{T}^{pk(n)}}{{A}_{k}})=\prod\limits_{i=0}^{k}{\mu ({{A}_{i}}).}$$
We formulate and prove a faithful version of this conjecture for mildly mixing systems and partially characterize, in the degree two case, the set of families 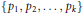 $\left\{ {{p}_{1}},{{p}_{2}},\,.\,.\,.\,,\,{{p}_{k}} \right\}$ satisfying the hypotheses of this theorem.
$\left\{ {{p}_{1}},{{p}_{2}},\,.\,.\,.\,,\,{{p}_{k}} \right\}$ satisfying the hypotheses of this theorem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
- 2
- Cited by

