Article contents
Frobenius Distribution for Quotients of Fermat Curves of Prime Exponent
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $C$ denote the Fermat curve over
$C$ denote the Fermat curve over 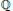 $\mathbb{Q}$ of prime exponent
$\mathbb{Q}$ of prime exponent  $l$ . The Jacobian
$l$ . The Jacobian 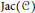 $\text{Jac(}C\text{)}$ of
$\text{Jac(}C\text{)}$ of  $C$ splits over
$C$ splits over 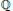 $\mathbb{Q}$ as the product of Jacobians
$\mathbb{Q}$ as the product of Jacobians  $\text{Jac(}{{C}_{k}})$ ,
$\text{Jac(}{{C}_{k}})$ , 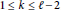 $1\,\le \,k\,\le \,\ell \,-\text{2}$ , where
$1\,\le \,k\,\le \,\ell \,-\text{2}$ , where 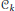 ${{C}_{k}}$ are curves obtained as quotients of
${{C}_{k}}$ are curves obtained as quotients of  $C$ by certain subgroups of automorphisms of
$C$ by certain subgroups of automorphisms of  $C$ . It is well known that
$C$ . It is well known that  $\text{Jac(}{{C}_{k}}\text{)}$ is the power of an absolutely simple abelian variety
$\text{Jac(}{{C}_{k}}\text{)}$ is the power of an absolutely simple abelian variety 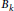 ${{B}_{k}}$ with complex multiplication. We call degenerate those pairs
${{B}_{k}}$ with complex multiplication. We call degenerate those pairs 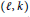 $(l,\,k)$ for which
$(l,\,k)$ for which 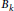 ${{B}_{k}}$ has degenerate
${{B}_{k}}$ has degenerate  $\text{CM}$ type. For a non-degenerate pair
$\text{CM}$ type. For a non-degenerate pair 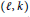 $(l,\,k)$ , we compute the Sato–Tate group of
$(l,\,k)$ , we compute the Sato–Tate group of  $\text{Jac(}{{C}_{k}}\text{)}$ , prove the generalized Sato–Tate Conjecture for it, and give an explicit method to compute the moments and measures of the involved distributions. Regardless of whether
$\text{Jac(}{{C}_{k}}\text{)}$ , prove the generalized Sato–Tate Conjecture for it, and give an explicit method to compute the moments and measures of the involved distributions. Regardless of whether 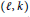 $(l,\,k)$ is degenerate, we also obtain Frobenius equidistribution results for primes of certain residue degrees in the
$(l,\,k)$ is degenerate, we also obtain Frobenius equidistribution results for primes of certain residue degrees in the  $l$ -th cyclotomic field. Key to our results is a detailed study of the rank of certain generalized Demjanenko matrices.
$l$ -th cyclotomic field. Key to our results is a detailed study of the rank of certain generalized Demjanenko matrices.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 4
- Cited by

