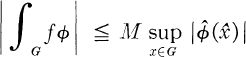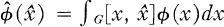Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Feichtinger, Hans G.
1981.
On a new Segal algebra.
Monatshefte f�r Mathematik,
Vol. 92,
Issue. 4,
p.
269.
Feichtinger, Hans G.
1981.
Functional Analysis and Approximation.
p.
153.
Maserick, P. H.
1981.
Disintegration with respect to L p-density functions and singular measures.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 57,
Issue. 3,
p.
311.
Fournier, John J. F.
1983.
On the Hausdorff-Young theorem for amalgams.
Monatshefte f�r Mathematik,
Vol. 95,
Issue. 2,
p.
117.
Bloom, Walter R.
1984.
Probability Measures on Groups VII.
Vol. 1064,
Issue. ,
p.
1.
Feichtinger, Hans G.
and
Gröbner, Peter
1985.
Banach Spaces of Distributions Defined by Decomposition Methods, I.
Mathematische Nachrichten,
Vol. 123,
Issue. 1,
p.
97.
Fournier, John J. F.
and
Stewart, James
1985.
Amalgams of 𝐿^{𝑝} and 𝑙^{𝑞}.
Bulletin of the American Mathematical Society,
Vol. 13,
Issue. 1,
p.
1.
Stewart, James
and
Watson, Saleem
1985.
Which amalgams are convolution algebras?.
Proceedings of the American Mathematical Society,
Vol. 93,
Issue. 4,
p.
621.
Myasnikov, A. G.
and
Chernykh, S. I.
1986.
Spaces Lp with a mixed norm on locally compact groups.
Functional Analysis and Its Applications,
Vol. 19,
Issue. 3,
p.
224.
Feichtinger, Hans G.
1987.
Banach Spaces of Distributions Defined by Decomposition Methods II.
Mathematische Nachrichten,
Vol. 132,
Issue. 1,
p.
207.
De Squire, Maria Torres
1993.
Multipliers from spaces of test functions to amalgams.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 54,
Issue. 1,
p.
97.
Mertens, Jean-François
and
Rubinchik, Anna
2014.
Essential properties of spaces (the amalgams) and the implicit function theorem for equilibrium analysis in continuous time.
Journal of Mathematical Economics,
Vol. 50,
Issue. ,
p.
187.
Butzer, Paul L.
Schmeisser, Gerhard
and
Stens, Rudolf L.
2016.
Sobolev spaces of fractional order, Lipschitz spaces, readapted modulation spaces and their interrelations; applications.
Journal of Approximation Theory,
Vol. 212,
Issue. ,
p.
1.
Auscher, Pascal
and
Prisuelos-Arribas, Cruz
2017.
Tent space boundedness via extrapolation.
Mathematische Zeitschrift,
Vol. 286,
Issue. 3-4,
p.
1575.
Jakobsen, Mads S.
2018.
On a (No Longer) New Segal Algebra: A Review of the Feichtinger Algebra.
Journal of Fourier Analysis and Applications,
Vol. 24,
Issue. 6,
p.
1579.
Unal, Cihan
and
Aydin, Ismail
2019.
On some compact embeddings of a weighted space.
Tbilisi Mathematical Journal,
Vol. 12,
Issue. 2,
Coulibaly, Sekou
and
Fofana, Ibrahim
2019.
On Lebesgue Integrability of Fourier Transforms in Amalgam Spaces.
Journal of Fourier Analysis and Applications,
Vol. 25,
Issue. 1,
p.
184.
Ablé, Z. V. P.
and
Feuto, J.
2019.
Duals of Hardy Amalgam Spaces and Norm Inequalities.
Analysis Mathematica,
Vol. 45,
Issue. 4,
p.
647.
Abtahi, Fatemeh
Rejali, Ali
and
Sabzali, Navid
2020.
The amalgam space L(p,q)π$\begin{array}{} L^{\pi}_{(p,q)} \end{array}$(G) on IN-groups.
Mathematica Slovaca,
Vol. 70,
Issue. 1,
p.
125.
Ma, Jiao
and
Liu, Zongguang
2020.
Commutators of Singular Integral Operators and Lipschitz Functions on Amalgam Spaces.
Journal of Function Spaces,
Vol. 2020,
Issue. ,
p.
1.
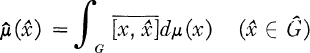
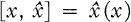 One answer to the question “Which functions can be represented as Fourier transforms of bounded measures?” was given by the following criterion due to Schoenberg [11] for the real line and Eberlein [5] in general: f is a Fourier transform of a bounded measure if and only if there is a constant M such that
One answer to the question “Which functions can be represented as Fourier transforms of bounded measures?” was given by the following criterion due to Schoenberg [11] for the real line and Eberlein [5] in general: f is a Fourier transform of a bounded measure if and only if there is a constant M such that