Hostname: page-component-65f69f4695-bd75b Total loading time: 0 Render date: 2025-06-28T21:07:21.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Fiber functors and reconstruction of Hopf algebras

Part of: Categories with structure Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  03 June 2024

Simon Lentner  and
Martín Mombelli
Simon Lentner
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Bundesstrassee 55, D20, 146 Hamburg, Deutschland e-mail: simon.lentner@uni-hamburg.de
Martín Mombelli*
Affiliation:
Facultad de Matemática, Astronomía y Física, Universidad Nacional de Córdoba, CIEM – CONICET, Medina Allende s/n, (5000) Ciudad Universitaria, Córdoba, Argentina
*
e-mail: martin.mombelli@unc.edu.ar
Get access Rights & Permissions [Opens in a new window]

Abstract

The main objective of the present paper is to present a version of the Tannaka–Krein type reconstruction theorems: if 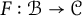$F:{\mathcal B}\to {\mathcal C}$ is an exact faithful monoidal functor of tensor categories, one would like to realize 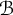${\mathcal B}$ as category of representations of a braided Hopf algebra 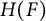$H(F)$ in 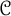${\mathcal C}$. We prove that this is the case iff 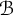${\mathcal B}$ has the additional structure of a monoidal 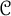${\mathcal C}$-module category compatible with F, which equivalently means that F admits a monoidal section. For Hopf algebras, this reduces to a version of the Radford projection theorem. The Hopf algebra is constructed through the relative coend for module categories. We expect this basic result to have a wide range of applications, in particular in the absence of fiber functors, and we give some applications. One particular motivation was the logarithmic Kazhdan–Lusztig conjecture.

Keywords

Tensor categoryfiber functorHopf algebra

MSC classification

Primary: 18D15: Closed categories (closed monoidal and Cartesian closed categories, etc.)
Secondary: 16T99: None of the above, but in this section

Information

Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 44
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The work of M.M. was partially supported by Secyt-U.N.C., Foncyt, and CONICET Argentina. S.L. thanks T. Gannon and T. Creutzig for hospitality at the University of Alberta and the Alexander von Humboldt Foundation for financial support via the Feodor Lynen Fellowship.

References

Andruskiewitsch, N. and Schneider, H.-J., On the classification of finite-dimensional pointed Hopf algebras . Ann. of Math. 171(2010), no. 1, 375–417.Google Scholar
Angiono, I. and Garcia Iglesias, A., Pointed Hopf algebras: a guided tour to the liftings . Rev. Colomb. Math. 53(2019), 1–44.Google Scholar
Bespalov, Y. N., Crossed modules, quantum braided groups and ribbon structures . Theor. Math. Phys. 103(1995), 368–387.Google Scholar
Bortolussi, N. and Mombelli, M., (Co)ends for representations of tensor categories . Theory Appl. Categ. 37(2021), no. 6, 144–188.Google Scholar
Bruguières, A. and Virelizier, A., Hopf monads . Adv. Math. 215(2007), 679–733.Google Scholar
Creutzig, T., Lentner, S., and Rupert, M., Characterizing braided tensor categories associated to logarithmic vertex operator algebras. Preprint, arXiv:2104.13262.Google Scholar
Creutzig, T., Lentner, S., and Rupert, M.. An algebraic theory for logarithmic Kazhdan–Lusztig correspondences. Preprint, arXiv:2306.11492.Google Scholar
Deligne, P., Catgories tannakiennes . In: The Grothendieck festschrift, Vol. II, Progress in Mathematics, 87, Birkhauser, Boston, MA, 1990, pp. 111–195.Google Scholar
Douglas, C. L., Schommer-Pries, C., and Snyder, N., The balanced tensor product of module categories . Kyoto J. Math. 59(2019), no. 1, 167–179.Google Scholar
Etingof, P. and Ostrik, V., Finite tensor categories . Mosc. Math. J. 4(2004), no. 3, 627–654.Google Scholar
Gannon, T. and Negron, C., Quantum SL(2) and logarithmic vertex operator algebras at (p,1)-central charge. Preprint, arXiv:2104.12821.Google Scholar
Husemöller, D., Lectures on tensor categories. Notes, Haverford College.Google Scholar
Liu, Z. and Zhu, S., Centers of braided tensor categories . J. Algebra 614(2023), 115–153.Google Scholar
Lyubashenko, V., Modular transformations for tensor categories . J. Pure Appl. Algebra 98(1995), 279–327.Google Scholar
Lyubashenko, V., Invariants of 3-manifolds and projective representations of mapping class groups via quantum groups at roots of unity . Commun. Math. Phys. 172(1995), no. 3, 467–516.Google Scholar
Lyubashenko, V., Squared Hopf algebras and reconstruction theorems . Banach Cent. Publ. 40(1997), 111–137.Google Scholar
Lyubashenko, V., Squared Hopf algebras, American Mathematical Society, Providence, RI, 1999.Google Scholar
Majid, S., Reconstruction theorems and rational conformal field theories . Int. J. Modern Phys. A 6(1991), 4359–4374.Google Scholar
Majid, S., Braided groups . J. Pure Appl. Algebra 86(1993), 187–221.Google Scholar
Majid, S., Cross products by braided groups and Bosonization . J. Algebra 163(1994), 165–190.Google Scholar
Radford, D. E., The structure of Hopf algebras with a projection . J. Algebra 92(1985), 322–374.Google Scholar
Rivano, N. S., Catégories tannakiennes . Bull. Soc. Math. France 100(1972), 417–430.Google Scholar
Schauenburg, P., Tannaka duality for arbitrary Hopf algebras, Algebra Berichte, 66, Reinhard Fischer, München, (1992).Google Scholar
Shimizu, K., The monoidal center and the character algebra . J. Pure Appl. Algebra 221(2017), no. 9, 2338–2371.Google Scholar
Shimizu, K., On unimodular finite tensor categories . Int. Math. Res. Not. 2017(2017), 277–322.Google Scholar
Takeuchi, M., Finite Hopf algebras in braided tensor categories . J. Pure Appl. Algebra 138(1999), no. 1, 59–82.Google Scholar