Published online by Cambridge University Press: 20 November 2018
Let q = p if p is an odd prime, q = 4 if p = 2. Let ζq be any primitive q-th root of unity, and let 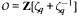 . We study the family of polynomials
. We study the family of polynomials 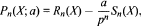 where Rn(X) and Sn(X) are the polynomials in the expansion
where Rn(X) and Sn(X) are the polynomials in the expansion 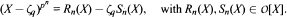 We show that for fixed n, Pn(X; a) is irreducible for all but finitely many a ∈ O, and for p = 3, we show that it is irreducible for all a ∈ O. The roots are all real and are permuted cyclically by a linear fractional transformation defined over the real pn-th cyclotomic field. From the roots we obtain a non-maximal set of independent units for the splitting field. In the last section we briefly treat extensions of our methods to composite p.
We show that for fixed n, Pn(X; a) is irreducible for all but finitely many a ∈ O, and for p = 3, we show that it is irreducible for all a ∈ O. The roots are all real and are permuted cyclically by a linear fractional transformation defined over the real pn-th cyclotomic field. From the roots we obtain a non-maximal set of independent units for the splitting field. In the last section we briefly treat extensions of our methods to composite p.