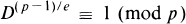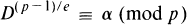Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lehmer, Emma
1989.
An indeterminate in number theory.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 46,
Issue. 3,
p.
469.
TANTI, JAGMOHAN
and
KATRE, S. A.
2010.
EULER'S CRITERION FOR SEPTIC NONRESIDUES.
International Journal of Number Theory,
Vol. 06,
Issue. 06,
p.
1329.
Katre, S A
and
Tanti, Jagmohan
2019.
Euler’s criterion for eleventh power nonresidues.
Proceedings - Mathematical Sciences,
Vol. 129,
Issue. 3,
Tanti, Jagmohan
2025.
Euler’s Criterion for prime order in some least non-PID cases.
The Ramanujan Journal,
Vol. 67,
Issue. 2,