Hostname: page-component-7f64f4797f-p4db6 Total loading time: 0 Render date: 2025-11-04T07:18:38.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Elements of Algebraic Geometry and the Positive Theory of Partially Commutative Groups

Published online by Cambridge University Press:  20 November 2018

Montserrat Casals-Ruiz  and
Ilya V. Kazachkov
Montserrat Casals-Ruiz
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, QC H3A 2K6, e-mail: casalsruiz@math.mcgill.ca, kazachkov@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The first main result of the paper is a criterion for a partially commutative group 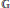$\mathbb{G}$ to be a domain. It allows us to reduce the study of algebraic sets over 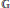$\mathbb{G}$ to the study of irreducible algebraic sets, and reduce the elementary theory of 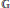$\mathbb{G}$ (of a coordinate group over 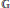$\mathbb{G}$ ) to the elementary theories of the direct factors of 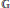$\mathbb{G}$ (to the elementary theory of coordinate groups of irreducible algebraic sets).

Then we establish normal forms for quantifier-free formulas over a non-abelian directly indecomposable partially commutative group 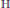$\mathbb{H}$ . Analogously to the case of free groups, we introduce the notion of a generalised equation and prove that the positive theory of 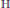$\mathbb{H}$ has quantifier elimination and that arbitrary first-order formulas lift from 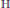$\mathbb{H}$ to 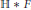$\mathbb{H}\,*\,F$ , where $F$ is a free group of finite rank. As a consequence, the positive theory of an arbitrary partially commutative group is decidable.

Keywords

20F1003C1020F06

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 3 , 01 June 2010 , pp. 481 - 519
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Baumslag, G., Myasnikov, A. G., and Remeslennikov, V. N., Algebraic geometry over groups I. Algebraic sets and Ideal Theory. J. Algebra 219(1999), no. 1, 16–79. doi:10.1006/jabr.1999.7881 Google Scholar
[2] Baumslag, G., Discriminating completions of hyperbolic groups. Geom. Dedicata 92(2002), 115–143. doi:10.1023/A:1019687202544 Google Scholar
[3] Brady, N., Short, H., and Riley, T., The Geometry of the Word Problem for Finitely Generated Groups. Advanced Courses in Mathematics. CRM Barcelona. Birkhauser Verlag, Basel, 2007.Google Scholar
[4] Charney, R., An introduction to right-angled Artin groups. Geom. Dedicata 125(2007), 141–158. doi: 10.1007/s10711-007-9148-6 Google Scholar
[5] Crisp, J. and Wiest, B., Embeddings of graph braid groups and surface groups in right-angled Artin groups and braid groups. Algebr. Geom. Topol. 4(2004), 439–472. doi:10.2140/agt.2004.4.439 Google Scholar
[6] Diekert, V., Gutierrez, C., and Hagenah, C., The existential theory of equations with rational constraints in free groups is PSPACE-complete. Inform. and Comput. 202(2005), no. 2, 105–140. doi:10.1016/j.ic.2005.04.002 Google Scholar
[7] Diekert, V., and Lohrey, M., Word equations over graph products. In: FST TCS 2003. Lecture Notes in Comput. Sci. 2450, Springer, Berlin, 2003, pp. 156–167.Google Scholar
[8] Diekert, V.,and Lohrey, M., Existential and positive theories of equations in graph products. Theory Comput. Syst. 37(2004), no. 1, 133–156. doi:10.1007/s00224-003-1110-x Google Scholar
[9] Diekert, V. and Muscholl, A., Solvability of equations in free partially commutative groups is decidable. Internat. J. Algebra Comput. 16(2006), no. 6, 1047–1070. doi:10.1142/S0218196706003372 Google Scholar
[10] Diekert, V. and Rozenberg, G., eds. The Book of Traces. World Scientific Publishing, River Edge, NJ, 1995.Google Scholar
[11] Duchamp, G. and Krob, D., Partially commutative Magnus transformations. Internat. J. Algebra Comput. 3(1993), no. 1, 15–41. doi:10.1142/S0218196793000032 Google Scholar
[12] Duncan, A. J., Kazachkov, I. V., and Remeslennikov, V. N., Centraliser dimension and universal classes of groups. Sib. Èlektron. Mat. Izv. 3(2006), no. 2, 197–215.Google Scholar
[13] Duncan, A. J., Centraliser dimension of partially commutative groups. Geom. Dedicata 120(2006), 73–97. doi:10.1007/s10711-006-9046-3 Google Scholar
[14] Duncan, A. J., Parabolic and quasiparabolic subgroups of free partially commutative groups. J. Algebra 318(2007), no. 2, 918–932. doi:10.1016/j.jalgebra.2007.08.032 Google Scholar
[15] Esyp, E. S., Kazachkov, I. V.,and Remeslennikov, V. N., Divisibility theory and complexity of algorithms for free partially commutative groups. In: Groups, Languages, Algorithms. Contemp. Math. 378. American Mathematical Society, Providence, RI, 2005, pp. 319–348.Google Scholar
[16] Feferman, S. and Vaught, L., The first order properties of products of algebraic systems. Fund. Math. 47(1959), 57–103.Google Scholar
[17] Hsu, T. and Wise, D., On linear and residual properties of graph products. Mich. Math. J. 46(1999), no. 2, 251–259. doi:10.1307/mmj/1030132408 Google Scholar
[18] Humphries, S., On representations of Artin groups and the Tits conjecture. J. Algebra 169(1994), no. 3, 847–862. doi:10.1006/jabr.1994.1312 Google Scholar
[19] Kharlampovich, O. and Myasnikov, A., Implicit function theorem over free groups. J. Algebra 290(2005), no. 1, 1–203. doi:10.1016/j.jalgebra.2005.04.001 Google Scholar
[20] Kvaschuk, A., Myasnikov, A. G., and Remeslennikov, V. N., Algebraic geometry over groups. III. Elements of Model Theory. J. Algebra 288(2005), no. 1, 78–98. doi:10.1016/j.jalgebra.2004.07.038 Google Scholar
[21] Makanin, G. S., Equations in a free group (Russian). Izv. Akad. Nauk SSSR, Ser. Mat. 46, 1199-1273, 1982. transl. in Math. USSR Izv., V. 21, 1983.Google Scholar
[22] Makanin, G. S., Decidability of the universal and positive theories of a free group. (Russian). Izv. Akad. Nauk SSSR Ser. Mat. 48(1984) no. 4, 735–749; Math. USSR Izv. 25(1985), no. 1, 75–88.Google Scholar
[23] Mal’cev, A. I., On the equation zxyx−1 y−1z−1 = aba−1b−1 in a free group. (Russian), Algebra i Logika Sem. 1(1962), no. 5, 45–50.Google Scholar
[24] Merzlyakov, Ju. I.. Positive formulae on free groups. Algebra i Logika Sem. 5(1966), no. 4, 25–42.Google Scholar
[25] Myasnikov, A. G. and Remeslennikov, V. N., Algebraic geometry over groups. II. Logical Foundations. J. Algebra 234(2000), no. 1, 225–276. doi:10.1006/jabr.2000.8414 Google Scholar
[26] Myasnikov, A. and Shumyatsky, P., Discriminating groups and c-dimension. J. Group Theory 7(2004), no. 1, 135–142. doi:10.1515/jgth.2003.039 Google Scholar
[27] Ol’shanskii, A. Yu., The Geometry of Defining Relations in Groups. [in Russian] Nauka, Moscow, 1989.Google Scholar
[28] Schulz, K., Makanin's algorithm for word equations–two improvements and a generalization. In: Word Equations and Related Topics. Lecture Notes in Comput. Sci. 572. Springer, Berlin, 1992, pp. 85–150.Google Scholar
[29] Shestakov, S. L., The equation [x, y] = g in partially commutative groups. Sibirsk. Mat. Zh. 46(2005), no. 2, 466-477; translation in Siberian Math. J. 46(2005), no. 2, 364–372.Google Scholar