If A is a set with only a finite number of elements, we write |A| for the number of elements in A. Let p be a large prime and let m be a positive integer fixed independently of p. We write [pm] for the finite field with pm elements and [pm]′ for [pm] – {0}. We consider in this paper only subsets H of [pm] for which |H| = h satisfies

1.1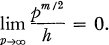

If f(x) ∈ [pm, x] we let N(f; H) denote the number of distinct values of y in H for which at least one of the roots of f(x) = y is in [pm]. We write d(d ≥ 1) for the degree of f and suppose throughout that d is fixed and that p ≧ p0(d), for some prime p0, depending only on d, which is greater than d.