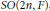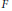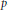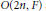Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jantzen, Chris
and
Liu, Baiying
2014.
The generic dual of p-adic split SO 2n and local langlands parameters.
Israel Journal of Mathematics,
Vol. 204,
Issue. 1,
p.
199.
Jantzen, Chris
2014.
Tempered representations for classical p-adic groups.
Manuscripta Mathematica,
Vol. 145,
Issue. 3-4,
p.
319.
Kim, Yeansu
2016.
Strongly positive representations of even GSpin groups.
Pacific Journal of Mathematics,
Vol. 280,
Issue. 1,
p.
69.
Tadić, Marko
2018.
Geometric Aspects of the Trace Formula.
p.
405.
Jantzen, Chris
2018.
Duality for classical 𝑝-adic groups: The half-integral case.
Representation Theory of the American Mathematical Society,
Vol. 22,
Issue. 6,
p.
160.
Jantzen, Chris
2018.
Jacquet modules and irrreducibility of induced representations for classical p-adic groups.
manuscripta mathematica,
Vol. 156,
Issue. 1-2,
p.
23.
Lust, Jaime
and
Stevens, Shaun
2020.
On depth zero L‐packets for classical groups.
Proceedings of the London Mathematical Society,
Vol. 121,
Issue. 5,
p.
1083.