Hostname: page-component-54dcc4c588-m259h Total loading time: 0 Render date: 2025-09-12T14:24:14.374Z Has data issue: false hasContentIssue false
  • English
  • Français

Differentiation of n-Dimensional Additive Processes

Published online by Cambridge University Press:  20 November 2018

M. A. Akcoglu  and
A. Del Junco
M. A. Akcoglu
Affiliation:
University of Toronto, Toronto, Ontario
A. Del Junco
Affiliation:
Ohio State University, Columbus, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let n ≧ 1 be an integer and let R n be the usual n-dimensional real vector space, considered together with all its usual structure. The usual n-dimensional Lebesgue measure on R n is denoted by λ n . The positive cone of R n is R n + and the interior of R n + is Pn . Hence Pn is the set of vectors with strictly positive coordinates. A subset of R n is called an interval if it is the cartesian product of one dimensional bounded intervals. If a, b ∊ R n then [a, b] denotes the interval {u|a ≦ u ≦ b|. The closure of any interval I is of the form [a, b]; the initial point of I will be defined as the vector a. The class of all intervals contained in R n + is denoted by 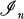. Also, for each u ∊ P n , let 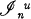be the set of all intervals that are contained in the interval [0, u] and that have non-empty interiors. Finally let en ∊ P n be the vector with all coordinates equal to 1.

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 3 , 01 June 1981 , pp. 749 - 768
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Akcoglu, M. A. and Chacon, R. V., A local ratio theorem, Can. J. Math. 22 (1970), 545–552.Google Scholar
2. Akcoglu, M. A. and Krengel, U., A differentiation theorem for additive processes, Math. Z. 163 (1978), 199–210.Google Scholar
3. Akcoglu, M. A. and Krengel, U., A differentiation theorem in Lp, Math. Z. 169 (1979), 31–40.Google Scholar
4. Akcoglu, M. A. and Sucheston, L., A ratio ergodic theorem for superadditive processes, Z. Wahr. und verw. Geb. 44 (1978), 269–278.Google Scholar
5. Dunford, N. and Schwartz, J. T., Convergence of almost everywhere of operator averages, J. Rat. Mech. and Anal. 5 (1956), 129–178.Google Scholar
6. Terrell, T. R., Local ergodic theorems for n-parameter semi-groups of operators, in Contributions to ergodic theory and probability, Lecture notes in Math. 160 (Springer-Verlag, 1970), 262–278.Google Scholar