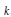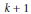Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Piguet, Diana
and
Saumell, Maria
2017.
A Median-Type Condition for Graph Tiling.
Electronic Notes in Discrete Mathematics,
Vol. 61,
Issue. ,
p.
979.
Jin, Ya-Lei
and
Zhang, Xiao-Dong
2018.
The number of maximal cliques and spectral radius of graphs with certain forbidden subgraphs.
Discrete Mathematics, Algorithms and Applications,
Vol. 10,
Issue. 06,
p.
1850071.
Hyde, Joseph
Liu, Hong
and
Treglown, Andrew
2019.
A Degree Sequence Komlós Theorem.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 4,
p.
2041.
Hladký, Jan
Hu, Ping
and
Piguet, Diana
2019.
Komlós's tiling theorem via graphon covers.
Journal of Graph Theory,
Vol. 90,
Issue. 1,
p.
24.
Piguet, Diana
and
Saumell, Maria
2019.
A median-type condition for graph tiling.
European Journal of Combinatorics,
Vol. 77,
Issue. ,
p.
90.
Hladký, Jan
Hu, Ping
and
Piguet, Diana
2021.
Tilings in graphons.
European Journal of Combinatorics,
Vol. 93,
Issue. ,
p.
103284.
Gan, Luyining
Han, Jie
Sun, Lin
and
Wang, Guanghui
2023.
Large Yk,b ${Y}_{k,b}$‐tilings and Hamilton ℓ $\ell $‐cycles in k $k$‐uniform hypergraphs.
Journal of Graph Theory,
Vol. 104,
Issue. 3,
p.
516.
Bai, Bo
Gao, Yu
Ma, Jie
and
Wu, Yuze
2024.
Phase Transitions of Structured Codes of Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 38,
Issue. 2,
p.
1902.
Li, Xihe
Ma, Jie
and
Zheng, Zhiheng
2025.
On the multicolor Turán conjecture for color-critical graphs.
Canadian Journal of Mathematics,
p.
1.
Hou, Jianfeng
Hu, Caiyun
Li, Heng
Liu, Xizhi
Yang, Caihong
and
Zhang, Yixiao
2025.
Toward a density Corrádi–Hajnal theorem for degenerate hypergraphs.
Journal of Combinatorial Theory, Series B,
Vol. 172,
Issue. ,
p.
221.
Hou, Jianfeng
Li, Heng
Liu, Xizhi
Yuan, Long-Tu
and
Zhang, Yixiao
2025.
A step towards a general density Corrádi–Hajnal theorem.
Canadian Journal of Mathematics,
p.
1.