Article contents
The Cubic Dirac Operator for Infinite-Dimensonal Lie Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 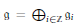 $\mathfrak{g}\,=\,{{\oplus }_{i\in \mathbb{Z}}}{{\mathfrak{g}}_{i}}$ be an infinite-dimensional graded Lie algebra, with dim
$\mathfrak{g}\,=\,{{\oplus }_{i\in \mathbb{Z}}}{{\mathfrak{g}}_{i}}$ be an infinite-dimensional graded Lie algebra, with dim 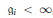 ${{\mathfrak{g}}_{i}}\,<\,\infty $ , equipped with a non-degenerate symmetric bilinear form
${{\mathfrak{g}}_{i}}\,<\,\infty $ , equipped with a non-degenerate symmetric bilinear form 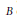 $B$ of degree 0. The quantum Weil algebra
$B$ of degree 0. The quantum Weil algebra 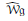 ${{\hat{\mathcal{W}}}_{\mathfrak{g}}}$ is a completion of the tensor product of the enveloping and Clifford algebras of
${{\hat{\mathcal{W}}}_{\mathfrak{g}}}$ is a completion of the tensor product of the enveloping and Clifford algebras of 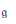 $\mathfrak{g}$ . Provided that the Kac–Peterson class of
$\mathfrak{g}$ . Provided that the Kac–Peterson class of 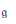 $\mathfrak{g}$ vanishes, one can construct a cubic Dirac operator
$\mathfrak{g}$ vanishes, one can construct a cubic Dirac operator 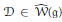 $\mathcal{D}\,\in \,\hat{\mathcal{W}}(\mathfrak{g})$ , whose square is a quadratic Casimir element. We show that this condition holds for symmetrizable Kac– Moody algebras. Extending Kostant's arguments, one obtains generalized Weyl–Kac character formulas for suitable “equal rank” Lie subalgebras of Kac–Moody algebras. These extend the formulas of G. Landweber for affine Lie algebras.
$\mathcal{D}\,\in \,\hat{\mathcal{W}}(\mathfrak{g})$ , whose square is a quadratic Casimir element. We show that this condition holds for symmetrizable Kac– Moody algebras. Extending Kostant's arguments, one obtains generalized Weyl–Kac character formulas for suitable “equal rank” Lie subalgebras of Kac–Moody algebras. These extend the formulas of G. Landweber for affine Lie algebras.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
- 1
- Cited by

