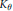Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alhajj, Rim
and
Fricain, Emmanuel
2024.
Composition operators on de Branges–Rovnyak spaces associated to a rational (not inner) function.
Journal of Mathematical Analysis and Applications,
Vol. 531,
Issue. 1,
p.
127811.
Liang, Yuxia
and
Partington, Jonathan R.
2025.
Composition operators between Toeplitz kernels.
Collectanea Mathematica,
Nasri, Mostafa
2025.
A Family of Surjective Composition Operators.
Results in Mathematics,
Vol. 80,
Issue. 3,