Hostname: page-component-6dbcb7884d-lhnfz Total loading time: 0 Render date: 2025-02-13T22:18:02.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Complemented Modular Lattices

Published online by Cambridge University Press:  20 November 2018

Ichiro Amemiya  and
Israel Halperin
Ichiro Amemiya
Affiliation:
Queen's University Tokyo College of Science
Israel Halperin
Affiliation:
Queen's University Tokyo College of Science
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

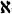1.1 This paper gives a lattice theoretic investigation of “finiteness“ and “continuity of the lattice operations” in a complemented modular lattice. Although we usually assume that the lattice is -complete for some infinite 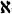,3 we do not require completeness and continuity, as von Neumann does in his classical memoir on continuous geometry (3); nor do we assume orthocomplementation as Kaplansky does in his remarkable paper (1).

1.2. Our exposition is elementary in the sense that it can be read without reference to the literature. Our brief preliminary § 2 should enable the reader to read this paper independently.

1.3. Von Neumann's theory of independence (3, Part I, Chapter II) leans heavily on the assumption that the lattice is continuous, or at least upper continuous.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 11 , 1959 , pp. 481 - 520
Copyright
Copyright © Canadian Mathematical Society 1959

References

1. Kaplansky, Irving, Any orthocomplemented complete modular lattice is a continuous geometry, Ann. Math., 61 (1955), 524-41.Google Scholar
2. Maeda, F., Kontinuierliche Geometrien (translation from the Japanese) (Berlin, Springer- Verlag, 1958).Google Scholar
3. von Neumann, J., Lectures on continuous geometry, Parts I, II, III, planographed (Princeton, The Institute For Advanced Study, 1935-7), to be reproduced in book form by Princeton University Press in 1959.Google Scholar
4. Sasaki, U., On an axiom of continuous geometry, J. Sci. Hiroshima Univ., Ser. A., 14 (1950), 100-1.Google Scholar