Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Yanping
Ding, Yong
and
Wang, Xinxia
2011.
Compactness for Commutators of Marcinkiewicz Integrals in Morrey Spaces.
Taiwanese Journal of Mathematics,
Vol. 15,
Issue. 2,
Chen, Yanping
and
Zhu, Kai
2015.
Weighted norm inequality for the singular integral with variable kernel and fractional differentiation.
Journal of Mathematical Analysis and Applications,
Vol. 423,
Issue. 2,
p.
1610.
Ding, Yong
and
Mei, Ting
2015.
Boundedness and Compactness for the Commutators of Bilinear Operators on Morrey Spaces.
Potential Analysis,
Vol. 42,
Issue. 3,
p.
717.
Chen, Jiecheng
and
Hu, Guoen
2015.
Compact Commutators of Rough Singular Integral Operators.
Canadian Mathematical Bulletin,
Vol. 58,
Issue. 1,
p.
19.
Guo, XiaoLi
and
Hu, GuoEn
2015.
Compactness of the commutators of homogeneous singular integral operators.
Science China Mathematics,
Vol. 58,
Issue. 11,
p.
2347.
Chen, Jiecheng
Chen, Yanping
and
Hu, Guoen
2015.
Compactness for the commutators of singular integral operators with rough variable kernels.
Journal of Mathematical Analysis and Applications,
Vol. 431,
Issue. 1,
p.
597.
Li, Peng
and
Zhou, Jiang
2016.
Compactness for the Commutator of the Multilinear Fourier Multiplier on the Morrey Space.
Acta Mathematica Vietnamica,
Vol. 41,
Issue. 4,
p.
661.
Meng, Siying
and
Chen, Yanping
2016.
Boundedness of homogeneous fractional integral operator on Morrey space.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
Chen, Yanping
Ding, Yong
and
Hong, Guixiang
2016.
Commutators with fractional differentiation and new characterizations of BMO-Sobolev spaces.
Analysis & PDE,
Vol. 9,
Issue. 6,
p.
1497.
Fu, Zun Wei
Trujillo, Juan J.
and
Wu, Qing Yan
2016.
WITHDRAWN: Riemann–Liouville fractional calculus in Morrey spaces and applications.
Computers & Mathematics with Applications,
Bokayev, Nurzhan
Burenkov, Victor
and
Matin, Dauren
2016.
On the pre-compactness of a set in the generalized Morrey spaces.
Vol. 1759,
Issue. ,
p.
020108.
Mao, Suzhen
and
Wu, Huoxiong
2016.
CHARACTERIZATION OF FUNCTIONS VIA COMMUTATORS OF BILINEAR FRACTIONAL INTEGRALS ON MORREY SPACES.
Bulletin of the Korean Mathematical Society,
Vol. 53,
Issue. 4,
p.
1071.
Bokayev, Nurzhan
and
Matin, Dauren
2017.
Functional Analysis in Interdisciplinary Applications.
Vol. 216,
Issue. ,
p.
44.
BU, Rui
CHEN, Jiecheng
and
HU, Guoen
2017.
Compactness for the commutator of Bochner-Riesz operator.
Acta Mathematica Scientia,
Vol. 37,
Issue. 5,
p.
1373.
Avsyankin, O. G.
2017.
On the compactness of convolution-type operators in Morrey spaces.
Mathematical Notes,
Vol. 102,
Issue. 3-4,
p.
437.
Авсянкин, Олег Геннадиевич
and
Avsyankin, Oleg Gennadievich
2017.
О компактности операторов типа свертки в пространствах Морри.
Математические заметки,
Vol. 102,
Issue. 4,
p.
483.
Bokayev, Nurzhan
Burenkov, Victor
and
Matin, Dauren
2017.
Sufficient conditions for the pre-compactness of sets in global Morrey-type spaces.
Vol. 1880,
Issue. ,
p.
030001.
Wang, Wei
and
Xu, Jingshi
2017.
Precompact Sets, Boundedness, and Compactness of Commutators for Singular Integrals in Variable Morrey Spaces.
Journal of Function Spaces,
Vol. 2017,
Issue. ,
p.
1.
Bokayev, Nurzhan
Matin, Dauren
and
Baituyakova, Zhuldyz
2018.
A sufficient condition for compactness of the commutators of Riesz potential on global Morrey-type space.
Vol. 1997,
Issue. ,
p.
020008.
Gürbüz, Ferit
2018.
Marcinkiewicz integrals with rough kernel associated with Schrödinger operators and commutators on generalized vanishing local Morrey spaces.
Tbilisi Mathematical Journal,
Vol. 11,
Issue. 3,
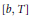 $\left[ b,\,T \right]$ for the singular integral operator on the Morrey spaces
$\left[ b,\,T \right]$ for the singular integral operator on the Morrey spaces 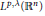 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ . More precisely, we prove that if
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ . More precisely, we prove that if 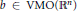 $b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$ , the
$b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$ , the 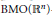 $\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ -closure of
$\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ -closure of 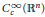 $C_{c}^{\infty }\left( {{\mathbb{R}}^{n}} \right)$ , then
$C_{c}^{\infty }\left( {{\mathbb{R}}^{n}} \right)$ , then 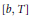 $\left[ b,\,T \right]$ is a compact operator on the Morrey spaces
$\left[ b,\,T \right]$ is a compact operator on the Morrey spaces 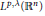 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for 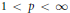 $1\,<\,p\,<\,\infty $ and
$1\,<\,p\,<\,\infty $ and 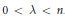 $0\,<\,\lambda \,<\,n$ . Conversely, if
$0\,<\,\lambda \,<\,n$ . Conversely, if 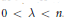 $b\,\in \,\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ and
$b\,\in \,\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ and 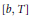 $\left[ b,\,T \right]$ is a compact operator on the
$\left[ b,\,T \right]$ is a compact operator on the 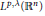 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for some
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for some 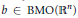 $p\,\left( 1\,<\,p\,<\,\infty\right)$ , then
$p\,\left( 1\,<\,p\,<\,\infty\right)$ , then 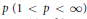 $b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$ . Moreover, the boundedness of a rough singular integral operator
$b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$ . Moreover, the boundedness of a rough singular integral operator 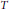 $T$ and its commutator
$T$ and its commutator 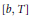 $\left[ b,\,T \right]$ on
$\left[ b,\,T \right]$ on 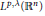 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ are also given. We obtain a sufficient condition for a subset in Morrey space to be a strongly pre-compact set, which has interest in its own right.
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ are also given. We obtain a sufficient condition for a subset in Morrey space to be a strongly pre-compact set, which has interest in its own right.
