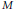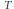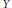Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
SUZUKI, Taro
and
TAKAKURA, Tatsuru
2009.
Asymptotic dimension of invariant subspace in tensor product representation of compact Lie group.
Journal of the Mathematical Society of Japan,
Vol. 61,
Issue. 3,