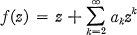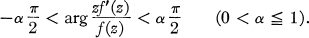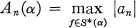Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shah, S. M.
1972.
Analytic functions with univalent derivatives and entire functions of exponential type.
Bulletin of the American Mathematical Society,
Vol. 78,
Issue. 2,
p.
154.
Leach, Ronald J.
1975.
On some classes of multivalent starlike functions.
Transactions of the American Mathematical Society,
Vol. 209,
Issue. 0,
p.
267.
Godula, Janusz
and
Nowak, Maria
1988.
Complex Analysis Joensuu 1987.
Vol. 1351,
Issue. ,
p.
140.
BRANNAN, D.A.
and
TAHA, T.S.
1988.
Mathematical Analysis and its Applications.
p.
53.
Rønning, Frode
1993.
Uniformly convex functions and a corresponding class of starlike functions.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 1,
p.
189.
Ali, Rosihan M.
and
Singh, Vikramaditya
1996.
On the fourth and fifth coefficients of strongly starlike functions.
Results in Mathematics,
Vol. 29,
Issue. 3-4,
p.
197.
Kiepela, K.
Pietrzyk, M.
and
Szynal, J.
2001.
The Sharp Bound for Some Coefficient Functional within the Class of Holomorphic Bounded Functions and Its Applications.
Rocky Mountain Journal of Mathematics,
Vol. 31,
Issue. 1,
Srivastava, H.M.
Mishra, A.K.
and
Gochhayat, P.
2010.
Certain subclasses of analytic and bi-univalent functions.
Applied Mathematics Letters,
Vol. 23,
Issue. 10,
p.
1188.
Frasin, B.A.
and
Aouf, M.K.
2011.
New subclasses of bi-univalent functions.
Applied Mathematics Letters,
Vol. 24,
Issue. 9,
p.
1569.
Ali, Rosihan M.
Lee, See Keong
Ravichandran, V.
and
Supramaniam, Shamani
2012.
Coefficient estimates for bi-univalent Ma-Minda starlike and convex functions.
Applied Mathematics Letters,
Vol. 25,
Issue. 3,
p.
344.
Xu, Qing-Hua
Gui, Ying-Chun
and
Srivastava, H.M.
2012.
Coefficient estimates for a certain subclass of analytic and bi-univalent functions.
Applied Mathematics Letters,
Vol. 25,
Issue. 6,
p.
990.
Srivastava, H. M.
2012.
Nonlinear Analysis.
Vol. 68,
Issue. ,
p.
607.
Porwal, Saurabh
and
Darus, M.
2013.
On a new subclass of bi-univalent functions.
Journal of the Egyptian Mathematical Society,
Vol. 21,
Issue. 3,
p.
190.
Aouf, M. K.
El-Ashwah, R. M.
and
Abd-Eltawab, Ahmed M.
2013.
New Subclasses of Biunivalent Functions Involving Dziok-Srivastava Operator.
ISRN Mathematical Analysis,
Vol. 2013,
Issue. ,
p.
1.
Magesh, N.
Rosy, T.
and
Varma, S.
2013.
Coefficient Estimate Problem for a New Subclass of Biunivalent Functions.
Journal of Complex Analysis,
Vol. 2013,
Issue. ,
p.
1.
Tang, Huo
Deng, Guan-Tie
and
Li, Shu-Hai
2013.
Coefficient estimates for new subclasses of Ma-Minda bi-univalent functions.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Peng, Z.
Murugusundaramoorthy, G.
and
Janani, T.
2014.
Coefficient Estimate of Biunivalent Functions of Complex Order Associated with the Hohlov Operator.
Journal of Complex Analysis,
Vol. 2014,
Issue. ,
p.
1.
Lee, See Keong
Ravichandran, V.
and
Supramaniam, Shamani
2014.
Initial Coefficients of Biunivalent Functions.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
El-Ashwah, R.M.
2014.
Subclasses of bi-univalent functions defined by convolution.
Journal of the Egyptian Mathematical Society,
Vol. 22,
Issue. 3,
p.
348.
Srivastava, H.M.
and
Bansal, Deepak
2015.
Coefficient estimates for a subclass of analytic and bi-univalent functions.
Journal of the Egyptian Mathematical Society,
Vol. 23,
Issue. 2,
p.
242.