Article contents
The Closure Ordering of Nilpotent Orbits of the Complex Symmetric Pair (SOp+q , SOp × SOq )
Published online by Cambridge University Press: 20 November 2018
Abstract
The main problem that is solved in this paper has the following simple formulation (which is not used in its solution). The group 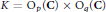 $K={{O}_{p}}\left( C \right)\times {{O}_{q}}\left( C \right)$ acts on the space
$K={{O}_{p}}\left( C \right)\times {{O}_{q}}\left( C \right)$ acts on the space 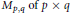 ${{M}_{p,\,q}}\,\text{of}\,p\,\times \,q$ complex matrices by
${{M}_{p,\,q}}\,\text{of}\,p\,\times \,q$ complex matrices by 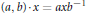 $\left( a,b \right)\cdot x=ax{{b}^{-1}}$ , and so does its identity component
$\left( a,b \right)\cdot x=ax{{b}^{-1}}$ , and so does its identity component  ${{K}^{0}}=\text{S}{{\text{O}}_{p}}\left( \text{C} \right)\times \text{S}{{\text{O}}_{\text{q}}}\left( \text{C} \right)$ . A
${{K}^{0}}=\text{S}{{\text{O}}_{p}}\left( \text{C} \right)\times \text{S}{{\text{O}}_{\text{q}}}\left( \text{C} \right)$ . A 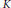 $K$ -orbit (or
$K$ -orbit (or 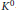 ${{K}^{0}}$ -orbit) in
${{K}^{0}}$ -orbit) in 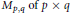 ${{M}_{p,q}}$ is said to be nilpotent if its closure contains the zero matrix. The closure,
${{M}_{p,q}}$ is said to be nilpotent if its closure contains the zero matrix. The closure, 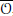 $\bar{\mathcal{O}}$ , of a nilpotent
$\bar{\mathcal{O}}$ , of a nilpotent 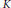 $K$ -orbit (resp.
$K$ -orbit (resp. 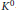 ${{K}^{0}}$ -orbit)
${{K}^{0}}$ -orbit) 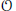 $\mathcal{O}$ in
$\mathcal{O}$ in 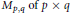 ${{M}_{p,q}}$ is a union of
${{M}_{p,q}}$ is a union of 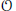 $\mathcal{O}$ and some nilpotent
$\mathcal{O}$ and some nilpotent 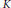 $K$ -orbits (resp.
$K$ -orbits (resp. 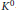 ${{K}^{0}}$ -orbits) of smaller dimensions. The description of the closure of nilpotent
${{K}^{0}}$ -orbits) of smaller dimensions. The description of the closure of nilpotent 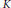 $K$ -orbits has been known for some time, but not so for the nilpotent
$K$ -orbits has been known for some time, but not so for the nilpotent 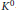 ${{K}^{0}}$ -orbits. A conjecture describing the closure of nilpotent
${{K}^{0}}$ -orbits. A conjecture describing the closure of nilpotent 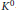 ${{K}^{0}}$ -orbits was proposed in
${{K}^{0}}$ -orbits was proposed in 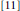 $[11]$ and verified when
$[11]$ and verified when 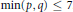 $\min \left( p,\,q \right)\le 7$ . In this paper we prove the conjecture. The proof is based on a study of two prehomogeneous vector spaces attached to
$\min \left( p,\,q \right)\le 7$ . In this paper we prove the conjecture. The proof is based on a study of two prehomogeneous vector spaces attached to 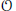 $\mathcal{O}$ and determination of the basic relative invariants of these spaces.
$\mathcal{O}$ and determination of the basic relative invariants of these spaces.
The above problem is equivalent to the problem of describing the closure of nilpotent orbits in the real Lie algebra 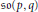 $\mathfrak{s}\mathfrak{o}\left( p,\,q \right)$ under the adjoint action of the identity component of the real orthogonal group
$\mathfrak{s}\mathfrak{o}\left( p,\,q \right)$ under the adjoint action of the identity component of the real orthogonal group 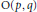 $\text{O}\left( p,\,q \right)$ .
$\text{O}\left( p,\,q \right)$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
- 4
- Cited by

