Article contents
Classification of homomorphisms from 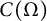 $C(\Omega)$ to a
$C(\Omega)$ to a 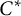 $C^*$-algebra
$C^*$-algebra
Published online by Cambridge University Press: 21 April 2025
Abstract
Let  $\Omega $ be a compact subset of
$\Omega $ be a compact subset of 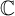 $\mathbb {C}$ and let A be a unital simple, separable
$\mathbb {C}$ and let A be a unital simple, separable 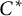 $C^*$-algebra with stable rank one, real rank zero, and strict comparison. We show that, given a Cu-morphism
$C^*$-algebra with stable rank one, real rank zero, and strict comparison. We show that, given a Cu-morphism 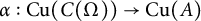 ${\alpha :\mathrm { Cu}(C(\Omega ))\to \mathrm {Cu}(A)}$ with
${\alpha :\mathrm { Cu}(C(\Omega ))\to \mathrm {Cu}(A)}$ with  , there exists a homomorphism
, there exists a homomorphism 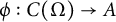 $\phi : C(\Omega )\to A$ such that
$\phi : C(\Omega )\to A$ such that 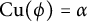 $\mathrm {Cu}(\phi )=\alpha $. Moreover, if
$\mathrm {Cu}(\phi )=\alpha $. Moreover, if 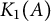 $K_1(A)$ is trivial, then
$K_1(A)$ is trivial, then  $\phi $ is unique up to approximate unitary equivalence. We also give classification results for maps from a large class of
$\phi $ is unique up to approximate unitary equivalence. We also give classification results for maps from a large class of 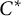 $C^*$-algebras to A in terms of the Cuntz semigroup.
$C^*$-algebras to A in terms of the Cuntz semigroup.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
The research of the first author was supported by NNSF of China (Grant No.: 12101113). The research of the second author was supported by NSERC of Canada. The third author was supported by LiaoNing Revitalization Talents Program (No.: XLYC2403058) and NNSF of China (Grant No.: 12101102).
References
- 1
- Cited by


