Article contents
Central Sequence Algebras of a Purely Infinite Simple C*-algebra
Published online by Cambridge University Press: 20 November 2018
Abstract
We are concerned with a unital separable nuclear purely infinite simple 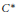 ${{C}^{*}}$ -algebra
${{C}^{*}}$ -algebra  $A$ satisfying UCT with a Rohlin flow, as a continuation of [12]. Our first result (which is independent of the Rohlin flow) is to characterize when two central projections in
$A$ satisfying UCT with a Rohlin flow, as a continuation of [12]. Our first result (which is independent of the Rohlin flow) is to characterize when two central projections in  $A$ are equivalent by a central partial isometry. Our second result shows that the
$A$ are equivalent by a central partial isometry. Our second result shows that the  $\text{K}$ -theory of the central sequence algebra
$\text{K}$ -theory of the central sequence algebra 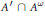 ${A}'\cap {{A}^{\omega }}$ (for an
${A}'\cap {{A}^{\omega }}$ (for an 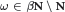 $\omega \in \beta \text{N}\!\!\backslash\!\!\text{N}$ ) and its fixed point algebra under the flow are the same (incorporating the previous result). We will also complete and supplement the characterization result of the Rohlin property for flows stated in [12].
$\omega \in \beta \text{N}\!\!\backslash\!\!\text{N}$ ) and its fixed point algebra under the flow are the same (incorporating the previous result). We will also complete and supplement the characterization result of the Rohlin property for flows stated in [12].
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
- 2
- Cited by

